Trig Identity
In this short challenge, can you use angle properties in a circle to figure out some trig identities?
Problem
Image
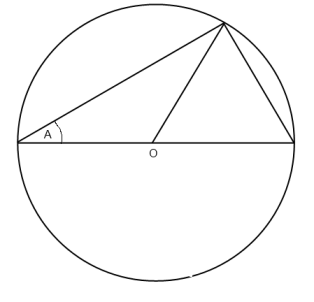
| In this diagram $O$ is the centre of a unit circle (i.e. a circle with radius 1). Use it to find two trigonometrical relationships between $A$ and $2A$. |
Did you know ... ?
Trigonometrical expressions can often be derived algebraically or geometrically. In more advanced applications the functions of trigonometry are defined as infinite power series rather than geometric ratios.
Getting Started
Here are some things you can try:
It's a good idea to draw out the diagram and include on it the facts that you know (such as the radius and the angle marked $A$).
The question mentions $2A$. Can you find an angle on your diagram which is equal to $2A$? (Hint - circle theorems may be useful!).
Trigonometry is also mentioned. Can you find a length equal to $\cos A$ or $\sin A$? It might be helpful to find some right-angled triangles.
The diagram below has some extra lines drawn on creating some right-angled triangles.

Student Solutions
We received several different solutions, all of which were correct and elegant.
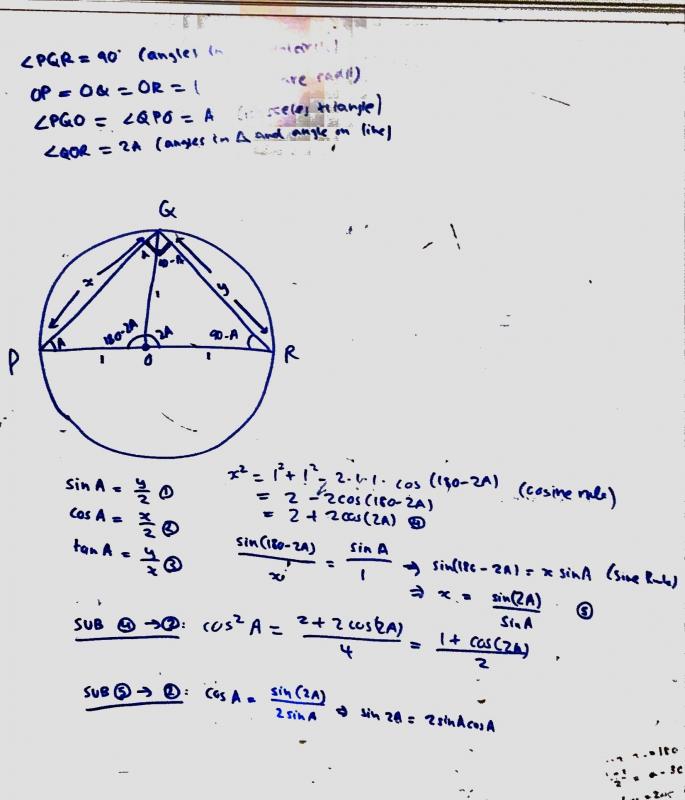
Joshua from Bohunt Sixth Form in the UK used the cosine rule and Pythagoras's Theorem. Click to see Joshua's work.

Soumya from King's Maths School used the cosine rule and the sine rule. Click to see Soumya's work.
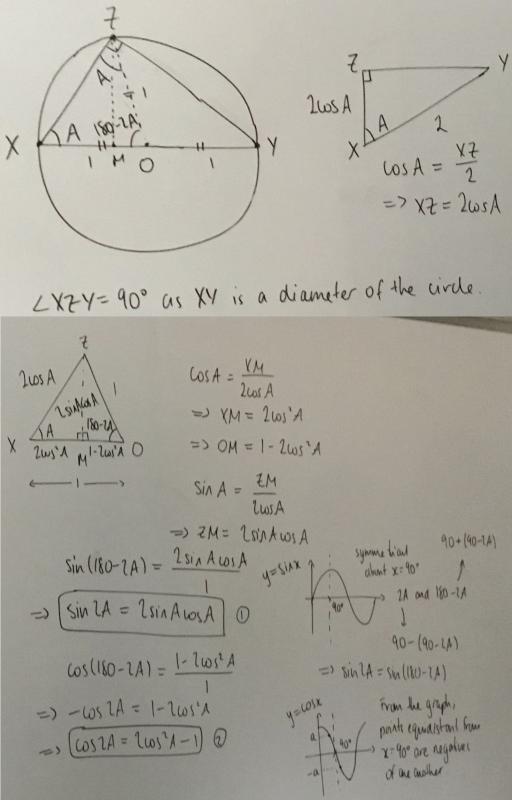
Dylan from Brooke Weston in the UK derived the formulas using the unlabelled angle from the original diagram. Click to see Dylan's work.
Nishad from Thomas Estley Community College in England split the triangles into lots of smaller right-angled triangles to prove the identities. Click to see Nishad's work.
Click on the image to see a larger version.

Teachers' Resources
Why do this problem?
This problem offers students the opportunity to find expressions for $\cos 2 A$ and $\sin 2 A$. They have to work out what they know, and what they can deduce given the information they have.
Students will need to bring together that they know about circle theorems, Pythagoras' theorem and properties of isosceles triangles to find the identities for $\cos 2A$ and $\sin 2A$.
Here are printable versions of the problem in Word and PDF format. They include extra diagrams for students to annotate.
Possible approach
Start with the diagram on the board and ask students if there are any angles or lengths they can put on the diagram given the information from the question.
Once the information from the question is on the diagram, ask students if there any other angles or lengths they can deduce. Ask them if they can find or create any right angled triangles.
Once the diagram has been adapted to show the lengths/angles that were known or could be deduced asked students if they can find a way to include $\sin 2A$ and/or $\cos 2A$ in a relationship involving a right-angled triangle.
Key questions
- What information are we given in the question?
- How we can display the information from the question on the diagram?
- What other angles can we deduce?
- Is there anything special about the two triangles on the diagram?
- What do you know about isosceles triangles?
- How many right-angled triangles can you find?
Possible extension
Students might like to explore T for tan which uses similar ideas to find some more trig identities.