Ford Circles
Can you find the link between these beautiful circle patterns and Farey Sequences?
Problem
In the interactivity below, you can move the sliders to choose values for $a, b, c$ and $d$. The circles have centres $\left(\frac{a}{c},\frac1{2c^2}\right)$ and $\left(\frac{b}{d},\frac1{2d^2}\right)$, and radii $\frac1{2c^2}$ and $\frac1{2d^2}$.
When the two circles touch, they are coloured in blue.
Explore the interactivity and find some values of $a, b, c$ and $d$ that generate circles that touch each other.
In the problem Farey Neighbours, you are invited to explore the value of $ad-bc$ for two adjacent fractions $\frac bd$ and $\frac ac$ from any Farey Sequence.
Explore the value of $ad-bc$ for the touching circles that you have found.
What do you notice?
Can you prove that for any touching circles in the interactivity above, $|ad-bc|=1$?
Can you prove that, given two such circles which touch the $x$ axis at $\frac bd$ and $\frac ac$, the circle with centre $\left(\frac{a+b}{c+d},\frac1{2(c+d)^2}\right)$ and radius $\frac1{2(c+d)^2}$ is tangent to both circles?
Getting Started
You might like to try the problem Baby Circle before attempting to prove the statements in this problem.
Student Solutions
Navjot from Sherborne Qatar School sent us a lovely clear explanation:
explore the value of $ad-bc$ for the touching circles that you have found. What do you notice?
I noticed that $ad-bc$ was always equal to $\pm 1$. This happened when the pair
of fractions were Farey neighbours.
For example, $\frac01, \frac 11: (0 \times 1) - (1 \times 1) = -1$
Or, $\frac 1{11}, \frac 1{12}: (1 \times 12) - (1 \times 11) =1$
In both of these cases, the two circles were tangent to each other.
Can you prove that for any touching circles in the interactivity above, $|ad-bc|=1$?
So it is given to us that the centre of circle $A$ is $\left(\frac ac , \frac1{2c^2}\right)$ with radius $\frac1{2c^2}$,
and the centre of circle B is $\left(\frac bd, \frac1{2d^2}\right)$ with radius
$\frac1{2d^2}$.
To show $|ad-bc| = 1$, I found the length between the centres of the two circles and equated it to the sum of the radii, which is also the length between the two points.
$|AB| =\sqrt{(\frac ac - \frac bd)^2 +(\frac1{2c^2} - \frac1{2d^2})^2)} = \frac1{2c^2} + \frac1{2d^2}$
$\Rightarrow \sqrt{\left(\frac{ad-bc}{cd}\right)^2 + \left(\frac{2d^2-2c^2}{4c^2d^2}\right)^2} = \frac{2d^2+2c^2}{4c^2d^2}$
$\Rightarrow \frac{(ad)^2 - 2abcd + (bc)^2}{(cd)^2}+ \frac{4d^4-8(dc)^2 + 4c^4}{16(cd)^4} = \frac{4d^4+8(dc)^2+4c^4}{16(cd)^4}$
$\Rightarrow \frac{(ad)^2 - 2abcd +(bc)^2}{(cd)^2}=\frac{(4d^4 + 8(dc)^2 + 4c^4) - (4d^4 - 8(dc)^2 + 4c^4)}{16(cd)^4}$
$\Rightarrow \frac{(ad-bc)^2}{(cd)^2} = \frac{16(cd)^2}{16(cd)^4}$
$\Rightarrow (ad-bc)^2=1$
$\Rightarrow |ad-bc|=1$.
We also received solutions from Sarith from Royal College in Sri Lanka, and Vignesh from Hymers College in the UK. You can read their solutions below:
Sarith's Solution
Vignesh's Solution
Teachers' Resources
Why do this problem?
This problem provides a beautiful extension to Farey Neighbours and encourages students to explore the connection between a geometrical pattern and a numerical sequence.
Possible approach
It would be helpful if students were familiar with Farey Sequences and Farey Neighbours.
Start by demonstrating the first GeoGebra applet and defining Ford Circles:
"Ford Circles have centre $\left(\frac{p}{q},\frac1{2q^2}\right)$ and radius $\frac1{2q^2}$, where $\frac{p}{q}$ is a fraction in its simplest form (that is, $p$ and $q$ are coprime integers)."
Invite students to explore the second GeoGebra applet and challenge them to find some values of $a, b, c$ and $d$ that generate circles which touch. Record any that they find, and invite them to look for patterns, drawing attention to $ad-bc$ if it does not emerge from the class.
The two questions at the end of the problem are the key to the link between Ford Circles and Farey Sequences, and provide a good challenge in proof for older students:
- Can you prove that for any touching circles in the interactivity, $|ad-bc|=1$
- Can you prove that, given two such circles which touch the $x$ axis at $\frac bd$ and $\frac ac$, the circle with centre $\left(\frac{a+b}{c+d},\frac1{2(c+d)^2}\right)$ and radius $\frac1{2(c+d)^2}$ is tangent to both circles?
A diagram like this one might help:
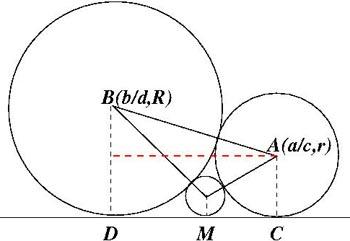
$R=\frac{1}{2d^2}$ and $r=\frac{1}{2c^2}$.
The centre of the circle which touches the horizontal axis at $M$ is $(\frac{a+b}{c+d}, \frac{1}{2(c+d)^2})$.
Key questions
What can you say about $R+r$ and $R-r$ if the circles centre $B$ and $A$ just touch each other?
Can you use Pythagoras theorem?
Possible extension
Students may wish to read more about Ford Circles in this Wikipedia article.
Possible support
As well as working on Farey Neighbours, Baby Circle would be a useful problem to try before attempting this challenging task.
