Baby circle
A small circle fits between two touching circles so that all three
circles touch each other and have a common tangent? What is the
exact radius of the smallest circle?
Age
16 to 18
Challenge level
Problem
Image
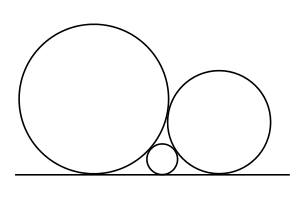
A circle with radius 1 and a circle with radius 2 touch at a point. A third circle fits between these two circles so that all three touch each other and all three have a common tangent. What is the radius of the smallest circle?
Getting Started
Student Solutions
Image
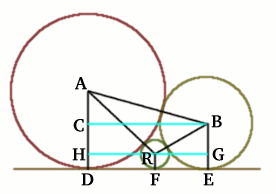
Rosalind of Madras College sent in this solution, well done Rosalind.
All three circles touch each other and have a common tangent $DFE$. The radius of the baby circle is $r$ and the radii of the other circles are $BE = 1$ unit and $AD = 2$ units. So $AC = 1$ unit, $AB = 3$ units, $AH = 2 - r$, $AR = 2 +r$, $BR = 1 + r$ and $BG = 1 - r$. Using Pythagoras Theorem: $$\eqalign{ \; RG &=& \sqrt{(1+r)^2 - (1-r)^2} = \sqrt{4r} = 2\sqrt{r} \\ \; HR &=& \sqrt{(2+r)^2 - (2-r)^2} = \sqrt{8r} = 2\sqrt{2r} \\ \; CB &=& 2\sqrt{2} = DE \\ RG + HR = CB &\Rightarrow& 2\sqrt{r} + 2\sqrt{2r} = 2\sqrt{2}.}$$ This gives $\sqrt{r}(1+\sqrt{2}) = \sqrt{2}$ and hence by squaring $$\eqalign{ r &=& \frac{2}{3+2\sqrt{2}} \\ \; &=& \frac{2(3 - 2\sqrt{2})}{(3+2\sqrt{2})(3-2\sqrt{2})} \\ \; &=& \frac{6 - 4\sqrt{2}}{9 - 4\times2} \\ \; &=& 6 - 4\sqrt{2}}$$ So the radius of the `baby circle` is $6 - 4\sqrt{2}$.