Building up friction
A series of activities to build up intuition on the mathematics of
friction.
Problem
This problem consists of a sequence of ideas concerning the configuration of hoop and pole as shown in the diagram below.
|
Image
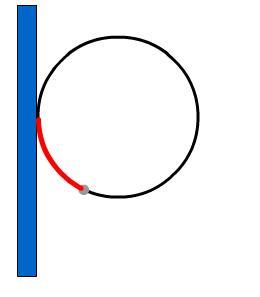
|
A rigid hoop of radius $r$ is attached to a vertical pole. A light ideal spring of unstretched length $L$ and spring constant $k$ is attached at one end at the point of contact of the hoop to the pole. A bead of mass $m$ is attached to the other end of the spring and the bead and spring are threaded onto the hoop, so they can slide around its circumference. |
If the hoop configuration is frictionless, what will be the possible range of positions of the bead for a stationary configuration?
What constants in the problem will affect the locations of these stationary positions? In particular, will they depend on the values of $r$ and $L$? Test your intuition by finding these values.
How will these results change if there is a coefficient of friction $\mu$ between the bead and the hoop? (The spring sliding around the hoop remains frictionless).
Can values of the constants be found so that the bead can remain stationary at any point on the hoop? Back up your conjecture with a mathematical analysis.
Imagine that the bead is stretched to a certain position and released. How many qualitatively different types of motion might result?
Student Solutions
The way to solve these kinds of unusual mechanics problems is to step back from the maths and consider the physical sense.
I found it useful not to worry about the "measure the angle from the horizontal" idea and use my own logical angles for each of the bead positions, and then worry about converting those solutions to a standard angle from the horizontal later.
I first considered four possible positions:
(1) the spring down, extended, with the bead in the third quadrant,
(2) finely balanced, touching the wall, at 180$^{\circ}$ (but this requires a "perfect" spring with no minimum length,
(3) the spring up, contracted from the unstretched length, with the bead in the second quadrant,
(4) the spring extended over the top, with the bead hanging in the first or fourth quadrant,
and drew a diagram of these.
Image

I then looked at the mechanics of each of these positions:
(1) measuring an angle $\theta$ clockwise from the downward vertical, $mg\sin(\theta) = kx$, where extension $x = r(\frac{\pi}{2} - \theta) - L \quad (0 < \theta < \frac{\pi}{2})$, where L is the unstretched length.
(2) is finely balanced
(3) measuring an angle $\alpha$ anti-clockwise from the upward vertical, $mg\sin(\alpha) = kx$, where extension $x = L - r(\frac{\pi}{2} - \alpha) \quad (0 < \alpha < \frac{\pi}{2})$.
(4) measuring an angle $\beta$ clockwise from the upward vertical, $mg\sin(\beta) = kx$, where extension $x = r(\frac{\pi}{2} + \beta) - L \quad (0 < \beta < \pi)$.
So the locations depend on $r$, $k$, and $L$.
Considering the case when there is friction between the bead and the rail, I drew a simple diagram with the forces.
Image

The limiting friction $F = \mu N$, where $N$ is the normal force between the bead and the rail.
I considered each extreme, when the limiting friction was pointing in each direction.
Position (1):
At furthest extension:
$$kx = mg \sin(\theta) + \mu mg\cos(\theta) = mg \left( \sin(\theta) + \mu \cos(\theta) \right)$$
$$\therefore r \left( \frac{\pi}{2} - \theta \right) - L = \frac{mg}{k} \left( \sin(\theta) + \mu \cos(\theta) \right)$$
At least extension:
$$kx + \mu mg\cos(\theta) = mg\sin(\theta)$$
$$\therefore r \left( \frac{\pi}{2} - \theta \right) - L = \frac{mg}{k} \left( \sin(\theta) - \mu \cos(\theta) \right)$$
So for $\theta = 0 \Rightarrow r\frac{\pi}{2} - L = \frac{mg \mu}{k}$ and for $\theta = \frac{\pi}{2} \Rightarrow -L = \frac{mg}{k}$. These are only compatible if (sub)
$$r\frac{\pi}{2} - L = -L\mu$$
$$\therefore r = \frac{2L}{\pi}(1 - \mu)$$
So now I'll check another location to see if this is compatible with the other location! Then we'll know whether it's possible to have these constants such that the bead can rest at any location.
Position (3):
Image

At furthest extension:
$$kx = mg\sin(\alpha) - \mu mg\cos(\alpha)$$
$$\therefore L - r \left( \frac{\pi}{2} - \alpha \right) = \frac{mg}{k} \left( \sin(\alpha) - \mu \cos(\alpha) \right)$$
At least extension:
$$kx = mg\sin(\alpha) + \mu mg\cos(\alpha)$$
$$\therefore L - r \left( \frac{\pi}{2} - \alpha \right) = \frac{mg}{k} \left( \sin(\alpha) + \mu\cos(\alpha) \right)$$
So for $\theta = 0 \Rightarrow L - r \frac{\pi}{2} = \frac{mg}{k}(-\mu)$ and for $\theta = \frac{\pi}{2} \Rightarrow L = \frac{mg}{k}$. So these are only compatible if (sub)
$$L - r\frac{\pi}{2}= -L\mu$$
$$\therefore r\frac{\pi}{2} = L(1 + \mu) \Rightarrow r = \frac{2L}{\pi}(1 + \mu)$$
So! This is only compatible with the formula found at position 1 ($r = \frac{2L}{\pi}(1 - \mu)$), if $\mu = 0$, i.e. if there is no friction. But we know that if there is no friction, the bead is only stable at the certain four positions.
Final part: types of motion:
For example, if the spring is stretched over the top and into the fourth quadrant, and then released, it might then:
1) fall further, oscillate about the lower centre, and either stop with friction, or not if frictionless.
2) stay put (i.e. it is in the equilibrium position, $kx = mg$ componented along the hoop)
3) move up, stop before the upper centre, oscillate up and down, and either stop with friction, or not if frictionless.
4) move up, past the upper centre, but oscillate back right past the centre, and stop with friction, or not if frictionless.
5) as (4) but staying on the left side.
Alternative solution
Part 1 - possible positions
If we assume that the spring cannot go more than once around the hoop, then we can divide the possible positions of the bead into 8 categories.
The first four involve the spring extending clockwise from the pole into each of the four quadrants
*Diagram*
If the bead is at rest in Quadrant 1, the spring must be contracted (if it were extended both gravity and the spring force would be acting in the same direction, and couldn't balance). Using similar arguments, in Quadrants 2 and 3 the spring would be extended, and in Quadrant 4 it would be very long, and contracted.
The second four involve the spring extending anti-clockwise from the pole
*Diagram*
This time, in Quadrant 4 the spring would be extended, in Quadrants 3 and 2 it would be contracted, and in Quadrant 1 it would be extended.
Part 2 - Frictionless case
Consider the forces acting on the bead in the tangential direction - the direction along the hoop - in the case where the spring runs clockwise. The gravitational force exerted by the mass of the bead in the compressing direction back along the spring is given by $m g \cos \theta$. [Note that in Quadrants 2 and 3, this will be a negative quantity, where gravity is actually pulling on the spring in the extending direction]. In addition, the spring force will be $k \times$ (current length of spring - $L$) , and this also acts back along the spring. [Again, when the spring is contracted, this will be negative, so the spring is being pushed in the extending direction]. Working out the length of the spring in terms of $\theta$ and $r$, and balancing these two forces gives the equation
$m g \cos \theta = k (L - \theta r)$
In the anti-clockwise spring case, the gravitaional force $m g \cos \phi$ will be acting in the extending direction, and so we get a slightly altered final equation
$m g \cos \phi = l (\phi r - L)$
Thus we can find solutions by looking for the crossing points of the following curves
*Diagram*
The key quantities are $\frac{mg}{k}$, $L$ and $L - 2 \pi r$.
Part 3 - with Friction
Friction will act to oppose the resultant of the gravitational and spring forces. Depending on the relative sizes of these forces sometimes friction will act in the compressing direction, and sometimes the extending direction.
Consider first the clockwise spring case: we find the normal force, in the direction perpendicular to the hoop's tangent, is given by $m g \sin \theta$. Thus friction is able to oppose the motion (and keep the bead still), as long as the resultant of the gravitational and spring forces is less than $\mid \mu m g \sin \theta \mid$. The stationary bead positions are given by any solutions to the equation
$k (L - \theta r) - m g \cos \theta = \alpha m g \sin \theta$
where $- \mu \leq \alpha \leq \mu$.
We can plot $ (L - \theta r) \pm \frac{\mu m g}{k} \sin \theta$, which gives the boundaries of the region in which friction can keep the bead still, against $\frac{mg}{k} \cos \theta$ to find solutions.
*Diagram*
For the anti-clockwise spring case, we instead find
$k (L - \phi r) + m g \cos \phi = \alpha m g \sin \theta$.
Question: can values of $L$, $m$, $k$ and $\mu$be found so that the bead can remain still at any position? Answer:
Part 4 - types of motion when bead released
