Rectangular pyramids
Problem
|
Is it true that $p^2+q^2=s^2+r^2$ when:
|
Image
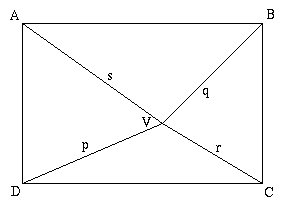
|
Getting Started
Think about right-angled triangles.
Student Solutions
A proof of this result came from students from the Key Stage 3 Maths Club at Strabane Grammar School, Northern Ireland and the following one from Joel, ACS (Barker) Singapore:
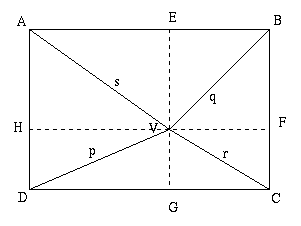
(a) In the diagram given (in 2 dimensions) p 2 + q 2 = r 2 + s 2
Proof
Draw 2 lines through V parallel to the edges of the rectangle, dividing the figure into four pairs of right-angled triangles. Label the point on AB as E, on BC as F, on CD as G and on DA as H. By Pythagoras theorem:
| p 2 = DG 2 +DH 2 |
| q 2 = BE 2 + BF 2 |
| r 2 = CF 2 + CG 2 |
| s 2 = AE 2 + AH 2 |
Since DG=AE, CG=BE, AH=BF and CF=DH,
p 2 + q 2 = AE 2 + CF 2 + CG 2 + AH 2 = r 2 + s 2
(b) If the diagram represents a pyramid on a rectangular base where p, q, r and s are the lengths of the sloping edges then the result p 2 + q 2 = r 2 + s 2 still holds true.
Proof
Let V 1 be the foot of the perpendicular from V to the base ABCD of the pyramid and let h be the height of the pyramid so that VV 1 = h and let V 1 A = s 1 , V 1 B = q 1 , V 1 C = r 1 , and V 1 D= p 1 .
By Pythagoras theorem we have: p 1 2 + h 2 = p 2 , q 1 2 + h 2 = q 2 , r 1 2 + h 2 = r 2 and s 1 2 + h 2 = s 2 .
Using the result already proved in 2dimensions, that is
p 1 2 + q 1 2 = r 1 2 + s 1 2 ,
we get p 1 2 + q 1 2 + 2h 2 = r 1 2 + s 1 2 + 2h 2
so p 2 + q 2 = r 2 + s 2 .
Teachers' Resources
Why do this problem?
It provides experience of generalising a result from 2 dimensions to an equivalent result in 3 dimensions. This problem asks the question for them but learners should be encouraged to ask themselves "What if..." and always to think about possible generalisations.Key questions
What comes to mind when a problem involves squares of distances?If we are looking for Pythagoras theorem where are the right angles triangles?
