Network Trees
Problem
A network is a collection of points and lines between the points. The points are called vertices and the lines which connect them are called edges. Each edge has a vertex at each end.
Here are some possible networks:
A connected network is a network in which we can get from any vertex to any other by travelling along the edges.
A planar network is one which can be redrawn in such a way that no edges cross each other.
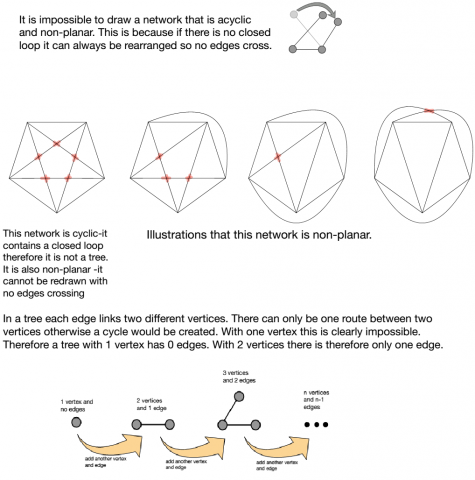
A cyclic network is one where there is a closed circuit or loop somewhere in the network. A network with no closed circuits is an acyclic network.
Describe each of the networks above with the words connected/disconnected, planar/non-planar and cyclic/acyclic.
2. Disconnected, Non-planar, Cyclic
3. Connected, Planar, Cyclic
4. Connected, Planar, Acyclic (note that this can be redrawn in such a way that the edges do not cross)
5. Connected, Planar, Acyclic
6. Connected, Planar, Cyclic
Draw a network which is Disconnected, Planar and Cyclic?
Can you draw a network which is Non-planar and Acyclic?
A network is called a tree if it is connected, planar and acyclic (like networks 4 and 5 above).
Investigate the number of edges in trees with different numbers of vertices.
Can you prove a relationship between the number of vertices in a tree and the number of edges?
Remember that the network must not be cyclic.
There are two different trees which have 4 vertices.

Note that the following two trees do not count as different as we can stretch each of them out as a straight line.

How many different trees can you draw with 5 vertices?
The degree of a vertex is the number of edges that meet at the vertex.

Draw all the possible trees with 2, 3 and 4 vertices.
Label the vertices on your drawings with the degree of each vertex.
Do the same for your trees with 5 vertices.
What can you say about the sum of the degrees of the vertices in trees with 2, 3, 4, 5, ... $n$ vertices?
Can you explain what you have noticed?
How does each edge contribute to the degrees of the vertices?
How many different trees can you draw with 6 vertices?
1, 1, 1, 1, 1, 5
1, 1, 1, 1, 2, 4
1, 1, 1, 1, 3, 3
1, 1, 1, 2, 2, 3
1, 1, 2, 2, 2, 2
One of these combinations produces more than one tree.
How many trees can you draw with 7 vertices?
How can you use your results so far to convince yourself that you have found all of the possible trees?
Getting Started
When drawing trees with 7 vertices, you might find it helpful to start by working out what the sum of the degrees of the 7 vertices must be.
Student Solutions
Nayanika from The Tiffin Girls' School in the UK sent in a solution which is an excellent start to this difficult problem. Click here to see Nayanika's solution with some notes about how the solution could continue.
John from Calthorpe Park Fleet in the UK built on Nayanika's ideas. Click to see John's solution.
Below the rest of John's solution is a rigorous proof that the number of edges in a network tree is 1 less than the number of vertices, submitted by Teiva. This is the rest of John's work:



Teiva sent in a proof that a network tree with $n$ vertices has $n-1$ edges. Teiva's proof has two parts.
Part A: Prove that every tree contains at least two vertices of degree 1
Part B: Use Part A and proof by induction to prove that a tree with $n$ vertices has $n-1$ edges
This is a more detailed structure of Teiva's proof. Click to see the Teiva's work for each step/stage.
Part A (lemma): Proof that every tree contains at least two vertices of degree 1, using the strong principle of induction
1. Check that the statement is true when $n=2$

2. Assume that the statement is true when $n=2,3,4,...,k$ for some whole number $k,$ and use this assumption to prove that the statement is true when $n=k+1$
- take a tree with $k+1$ vertices and select one of those vertices. If $d$ is the order of the vertex, then the vertex is connected to $d$ sub-networks via its $d$ edges.

- Prove that the $d$ sub-networks are all separate to each other and are all trees or single vertices
Secondly, we note that each sub-network is acyclic, as it is a sub-network of a tree (which is acyclic).
Hence, and using the previous point, each sub-network is either a lone vertex, or it is a tree.
- Use the assumption to prove that the network has at least two vertices of degree 1
Now, by the inductive hypothesis, each of these sub-trees contains at least 2 vertices of degree 1. Then either one of these is the explicitly drawn vertex (which is connected to V and is hence not a vertex of degree 1 in T), or not. In either case, a sub-tree contributes at least one vertex of degree 1, so that at least $t$ vertices of degree 1 are contributed to T. We can then note that if some sub-network is a lone vertex, then it is a vertex of degree 1.
Then if $d\ge2,$ our lemma is true for T. Otherwise (i.e. if $d=1$) then we note that V is itself a vertex of degree 1 to T, so that our lemma is true for T.
Hence since $d\ge1$ (because T is connected), our lemma is true for T and hence for any tree of $k+1$ vertices, so that our inductive argument is complete.
3. Conclude that this means the statement must be true for all whole numbers
That is, every tree contains at least two vertices of degree 1.
Part B: Proof that a tree with $n$ vertices has $n-1$ edges, using Part A and the weak principle of induction
1. Check that the statement is true when $n=2$
2. Assume that the statement is true when $n=k$ for some whole number $k,$ and use this assumption to prove that the statement is true when $n=k+1$
We investigate the sub-network structure:
Firstly, it is connected, as T is connected, and the extra vertex in T clearly does not create any new paths between vertices in the sub-network.
Secondly, it is acyclic, as it is a sub-network of a tree.
Hence, the sub-network is a tree, and is indeed clearly one of $k$ vertices.
Then, by the inductive hypothesis, this sub-tree contains exactly $k-1$ edges, so that T contains $(k-1)+1=(k+1)-1$ edges, and our theorem is hence true for all trees of $k+1$ vertices.
3. Conclude that this means the statement must be true for all whole numbers
That is, it is proven that all trees of $n$ vertices contain exactly $n-1$ edges.
Teiva added a further note:
Also, I'm almost positive that there's an argument to be made with an infinite walk to prove that every tree has a vertex of degree 1 (or else it would be cyclic), but I just can't nail it down properly. (Why does such a walk returning to a vertex imply a cycle?)
Imagine you start off at a vertex V of a tree, and trace a path ('go for a walk') along the edges of the tree. Either the path goes on forever (an 'infinite walk'), or it eventually ends. The only way it can go on forever is either if you have found a cycle (which may or may not involve passing back through V), or if there are infinitely many vertices. In each case, the network was not a tree. Therefore the walk must end. But it must end at a vertex with only 1 edge. Therefore the tree contains a vertex of degree 1.
Teachers' Resources
Why do this problem?
In introducing the idea of networks and graph theory this is one of the simplest results to prove. It gives learners practice in mathematical reasoning and an idea of what graphs are.
This problem can be used with KS4 students as an introduction to some of the topics covered in A-level Further Maths.
It can also be used as an introduction to the idea of induction (If we know that a graph with $n$ vertices has $n-1$ edges, what happens if we add an extra vertex?)
Possible approach
The idea of a network could be introduced through an example of connections between people (perhaps using the idea of "six degrees of Kevin Bacon" and linking some actors together via films that they have both starred in). Other real life networks, such as the London Undergorund Map, could be discussed.
You could also introduce alternative terms for some of the ideas introduced: graph for network, arc for edge, and node for vertex should be mentioned.
Consider the six given graphs and decide whether each one is connected/disconnected, planar/non-planar and cyclic/acyclic. Students could draw other networks which satisfy various conditions or could consider how the given graphs could be altered to make them connected, planar and acyclic.
Key questions
- What is the simplest network you can draw?
- Draw trees for networks with 1, 2, 3, 4, ... vertices. How many edges are needed?
- Does every tree for a network of 5 vertices have the same number of edges?
- Can you write down a rule connecting the number of edges and the number of vertices?
- If we add an extra vertex to a network, what happens to the number of edges? If we add an edge to a network, what happens to the number of vertices.
Possible support
Simply Graphs gives an introduction to networks where students can think about how they would categorise networks before being introduced to the definitions in this problem.
Learners might spend a little time playing the game Sprouts. Sprouts leads to much more graph theory than this one problem, and you can read more in the Sprouts Article.
Possible extension
The connections between networks and polyhedra, and a justification of Euler's Theorem, can be found in this problem.
Try the problem Plum Tree.
