Instant Insanity

Given the nets of 4 cubes with the faces coloured in 4 colours, build a tower so that on each vertical wall no colour is repeated, that is all 4 colours appear.

Magic Caterpillars

Label the joints and legs of these graph theory caterpillars so that the vertex sums are all equal.

Plum Tree

Label this plum tree graph to make it totally magic!

Simply Graphs

Stage: 5 Challenge Level:

A graph is a set of vertices (or nodes), together with a set of edges (or arcs).

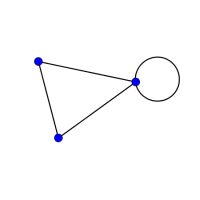
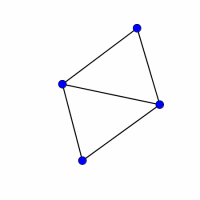
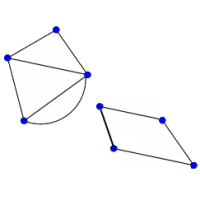
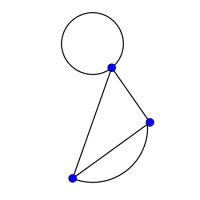
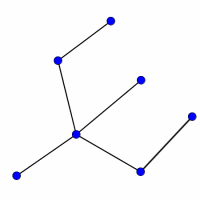
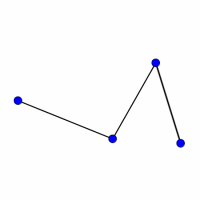
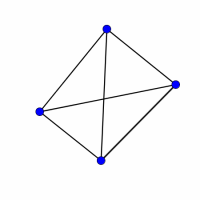
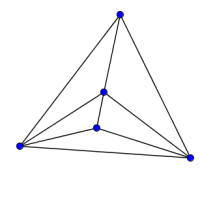
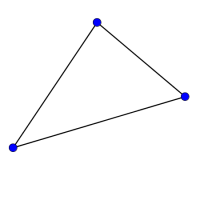
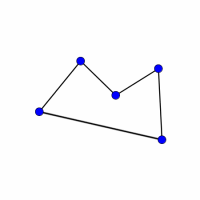
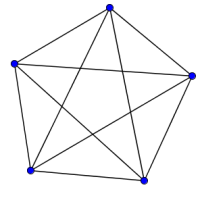
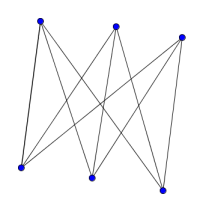
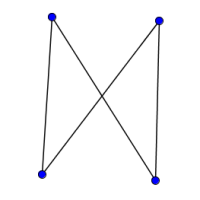
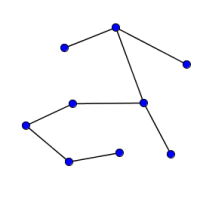
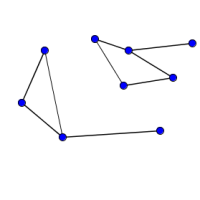
Look at the graphs below. You can print them off as a set of cards here.

Can you find graphs that you think 'belong' together in some sense?
Can you describe the features they have in common?
Could you draw more graphs that 'belong' in the same set?

Click below to see some definitions used to describe graphs.

A loop is an edge with the same vertex at both ends.
A simple graph has no loops, and there is no more than one edge connecting any pair of vertices. A multigraph has multiple edges connecting some pairs of vertices.
A walk is a sequence of edges in which the end of one edge (except the last) is the beginning of the next.
A trail is a walk in which no edge is repeated.
A path is a trail in which no vertex is repeated.
A cycle is a closed path (the end of the last edge is the start of the first).
A Hamiltonian cycle visits every vertex.
A connected graph has a path between every pair of vertices.
A tree is a simple connected graph with no cycles.
A complete graph is a simple graph where every pair of vertices is connected by an edge.

Can you find examples on the cards that match each definition? Can you draw some more examples of your own?

Games. Mathematical modelling. Combinatorics. Mathematical reasoning & proof. Visualising. Topology. Working systematically. Networks/Graph Theory.

You may also like

Instant Insanity

Magic Caterpillars

Plum Tree

Simply Graphs

Stage: 5 Challenge Level: