Sprouts explained
This article invites you to get familiar with a strategic game called "sprouts" which appears here on the NRICH site. The game is simple enough for younger children to understand, and has also provided experienced mathematicians with significant food for thought. After a description of the basic game, this article will
suggest a few ways to explore it.
The game
The game of Sprouts was invented in 1967 by two mathematicians John H. Conway and Michael S. Paterson, when they were both at the University of Cambridge in the UK. The game was popularised by one of Martin Gardner's "Mathematical Games" columns in Scientific American. Here is a quote from Conway:
"The day after sprouts sprouted, it seemed that everyone was playing it, at coffee or tea times, there were little groups of people peering over ridiculous to fantastic sprout positions."
Sprouts is a game for two players. All you really need is paper and a pencil.. The game starts by drawing any number of spots. In this example we are going to look at 3 spots.

The first player has a turn by joining two of the spots and marking a new spot in the middle of the line. Or the line may start and end on the same spot. 
Rules:
You are not allowed to draw a line which crosses another line. This is important to remember!
A spot cannot have more than three lines leading to or from it. For example, in the game below, spots A and B cannot be used any more because they already have three lines.
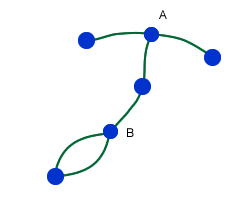
The idea is to make it impossible for the other player to draw a line.
So the last person to draw a line is the winner.
Over to you!
Find a friend to play the game with. We suggest that you limit the number of spots to 3. Try playing several games to get the hang of it. Here are a few questions to focus your mind, but don?t try to answer them until you have played the game a few times, and feel confident with the rules.
-
Does the person who goes first or second tend to win?
-
Can you explain any winning tactics?
-
The game must end after a limited number of moves. Explain why. (Hint: you might find it useful to explain this in terms of "liberties". The liberties of a spot equals 3 minus the number of lines drawn from that spot.)
Conway notation:
How did you explain the winning tactics? In discussing this game, several enthusists have found it helpful to adopt a form of notation to communicate their ideas and strategies. We often use notation to explain our ideas in mathematics, and you might find it interesting to learn a little about Conway notation, the official notation of the WGOSA (The World Game of Sprouts Association). It began to evolve in 1999 in a discussion on the mathforum website.
Extending the game to different numbers of spots:
The strategy becomes more complex as you increase the number of spots, although WGOSA suggests that live spots at the end of the game are the key to making the game fun to play. (A "live" spot is a spot that is not "dead". A "dead" spot has 3 lines attached to it and is therefore out of the game.) These live spots at game's end are called "survivors".
Suppose a normal sprouts game begins with an even number of spots. Which player is likely to win and what can you say about the number of survivors (1)? If the game started with an odd number of spots what would you expect to happen and what could you say about the number of survivors (2)?
Proofs to be explored:
There is quite a lot of nice mathematics that can be gleaned from the game. What follows is a look at a few proofs. Stephan Duerr has summarised some of these, and added his own at the web site given below.
Enthusiasts have come up with a terminology that is useful to the proofs. These are all given below:
-
The "liberties" of a spot equal three minus the number of lines emerging from the spot.
-
A spot is "dead" if it has no liberties.
-
A "survivor" is a live spot at game's end.
-
A "guard" is a dead spot that is one of the two nearest neighbours of a survivor (see more details below).
-
A "pharisee" is a dead spot that is not a guard.
-
A "region" is an area of white space on the paper bounded by lines. The region extending off to the horizon is called "outer region", all other regions are "inner regions". At game's start, there is one region.
-
A "cluster" (or "clump") consists of all spots that are directly or indirectly connected by lines. An "indirect" connection means that there are other spots along the connection. The smallest possible cluster consists of just one unattached spot. At the beginning of a game with n spots there are n clusters.
-
The lines emerging from a spot divide the area around the spot into "sites". Spots have as many sites as lines, except for no lines, where there is one site.
Let:
$n=$ number of spots at the beginning of the game
$d=$ number of dead spots
$m=$ number of moves
$s=$ number of survivors
$p=$ number of pharisees
$c=$ number of clusters
$r=$ number of regions
$L=$ number of liberties
A few to get your teeth into?
All of these proofs have been taken from work by contributors to the maths forum.
Prove that the number of liberties at any time can be expressed as $L=3n-m$
Each spot has $3$ liberties at the beginning of the game. There are $n$ spots. Hence at the beginning of the game there are $3n$ liberties.
Each move reduces the number of liberties by $1$. This is because the two spots that are joined result in $2$ liberties being lost, whilst the spot that is added results in $1$ liberty being added.
Hence $L=3n-m$.
Prove that the maximum number of moves can be expressed as $m\leq 3n-1$.
At the game's end, each survivor has exactly $1$ liberty (otherwise you could connect the survivor to itself), hence $s=3n-m$.
$s\geq 1$ hence $3n-m\geq 1$.
Rearranging this gives $3n-1\geq m$ or $m\leq 3n-1$.
Prove that the minimum number of moves can be expressed as $m\geq2n$.
At the end of a game, each survivor is surrounded by $2$ guards.
These guards are spots that are dead in one of two ways:
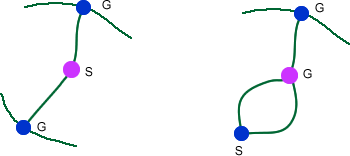
If any guard were live, the game could be continued by connecting the guard to the survivor. Each guard has at least two of its sites accessing a region that is also accessible to the survivor. Since no two survivors can access the same region (otherwise we could connect the survivors), no spot can be a guard for two different survivors.
A pharisee is a dead spot that is not a guard.
The number of pharisees is the total number of spots minus the number of survivors and minus the number of guards. Written algebraically:
$$p=n+m-s-2s$$ $$p=n+m-3s$$ $$p=n+m-3(3n-m)$$ $$p=n+m-9n+3m$$
Hence $p=4m-8n$
Rearranging this equation gives us $m=p/4 + 2n$.
If the game is played so that there are no Pharisees, that is a game is played with the minimum number of moves, then $m=2n$.
So we can say that $m\geq 2n$.
Prove that the maximum number of regions can be expressed as $r\leq 2n+1$
There are exactly two types of moves in sprouts. One type merges two clusters, the other type creates a new region.
Because the number of regions either increases by $1$ or the number of clusters decreases by $1$, we can deduce that each move increases $r-c$ by $1$, or that $r-c-m$ must be constant throughout the game.
At the beginning of a game, $r=1$, $c=n$ and $m=0$.
From this we can deduce that $r-c-m=1-n-0$ which can be rearranged to give: $$r=1-n+c+m$$
At the end of the game, as we have already seen, $s=3n-m$, or $m=3n-s$.
Substituting this equation into the above we have: $$r=1-n+c+3n-s$$ which simplifies to: $$r=2n+1+c-s$$ Every cluster must contain at least one live spot, namely the spot of the cluster that was last to be placed on the paper. From this we can say $c\leq s$.
As $c\leq s$, then $c-s\leq 0$. We can substitute this into $r=2n+1+c-s$ to give: $$r\leq 2n+1$$.
In conclusion
Sprouts is an intriguing game which contains some interesting mathematics. Have fun with the game, and may sprouts continue sprouting!
