Nineteen hexagons
In this maze of hexagons, you start in the centre at 0. The next
hexagon must be a multiple of 2 and the next a multiple of 5. What
are the possible paths you could take?
Problem
Here is a maze made from hexagons:
Image

You need to go from the centre to one of the outside hexagons in two steps.
You start in the centre at $0$.
The next hexagon you visit must be a multiple of $2$.
The next hexagon you visit must be a multiple of $5$.
What are the possible paths you could take?
This sheet of hexagons may be helpful.
Getting Started
It might be helpful to circle all the multiples of two in one
colour and all the multiples of five in another colour to start
with.
Choose one multiple of two that you could go to
first. Is there a multiple of five next to it on the
outside of the maze? Are there any others?
How are you going to record your paths so you know where
you've been?
Student Solutions
Thank you to those of you who sent in solutions - sorry that we can't mention everyone. Cong from St Peters RC School in Aberdeen shaded the hexagon grid which helped him to answer the question:
Image
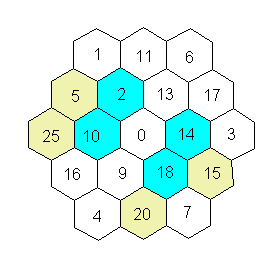
Cong says:
The multiples of $2$ are highlighted by blue. The multiples of $5$ are highlighted by yellow.The $6$ possible paths that you could take are:
$0$ to $2$ to $5$
$0$ to $10$ to $25$
$0$ to $10$ to $5$
$0$ to $14$ to $15$
$0$ to $18$ to $15$
$0$ to $18$ to $20$
Well done also to Liam and Daniel from Troon County Primary School, and Erika from the Chinese International School (to name just a few).
Teachers' Resources
Why do this problem?
This problem is a good way for children to gain familiarity with multiples of two and five. In addition, it encourages a systematic approach to problem solving by asking for all the possible routes.
It might be useful for children to mark all the multiples of two and five on a number line or number square before they start on the maze.
This sheet gives a number of small copies of the maze for rough working and recording the various routes. This blank grid may be useful for pupils to make their own
mazes.
Key questions
Have you marked all the multiples of two and five on your number line/ number square?
Would it be a good idea to circle all the multiples of two in red and all the multiples of five in blue to start with?
Can you see an even number/multiple of two?
How can you tell that a number is a multiple of five/in the five times table?
Where can you go from here?
How many ways have you found so far? Can you see any other ways?
How are you going to record your paths so you know where you've been?
