Stars
Can you work out what step size to take to ensure you visit all the dots on the circle?
Problem
There are printable circles of dots on the NRICH Printable Resources page, under Circle templates > Without central point
Draw some stars using the interactivity below.
Choose how many points you would like around your circle
Now choose a starting point and drag to another point. Watch as the pattern continues to travel around the circle...
When a circle has 8 dots you can move around the circle in steps of length $1$, $2$, $3$, $4$, $5$, $6$ or $7$.
If you move around the circle in steps of $2$, you miss some points
If you move around the circle in steps of $3$, you visit all the points.
How else can you visit all the points?
When a circle has $9$ dots there are $6$ different step sizes where you visit every point.
Which step sizes allow you to do this?
Now consider $10$ points. Can you find the $4$ different step sizes in which we can visit every point?
Explore what happens with different numbers of points and different step sizes.
How can you work out what step sizes will visit all the points for any given number of points?
Now consider $5$ points. You can visit all the points irrespective of the step size. Which other numbers have this property?
Can you find a relationship between the number of dots on the circle and the number of steps that will ensure that all points are hit?
If you would rather work on paper, go to the Printable Resources page to open PDF files of the circles (Circle templates > Without central point)
Each PDF file contains 12 identical circles with a specific number of dots. You can select any number of dots from 3 to 24.
Getting Started
Keep a record of your results.
Try to find out what is special about the step sizes when you don't hit all the points.
Student Solutions
Explore what happens with different numbers of points and different step sizes. How can you work out what step sizes will visit all the points for any given number of points?
Paul from Test Valley Secondary School wrote:
If you set the Points to 8 and make the step size 3 it will hit all points.
The [angles in the] points between the edges of the stars are exactly 45 degrees. So 45 degrees $\times$ 8 (the number points) is 360 degrees, the angle of a circle. It will work no matter how many points you have.
Joshua from Davenies in England and Cameron, Jes and Vihan from ISZN in Switzerland thought about odd and even numbers of dots. Joshua wrote:
If the number of dots around the edge is odd then the number of steps can be odd or even. If the number of dots around the edge is even then the number of steps can only be odd otherwise it will go in an infinite loop in the same shape and on the same dots.
Cameron, Jes and Vihan continued:
This is because with jumps of two, half of the dots will be missed in the first round and if the number of jumps is a factor of the number of dots, then it will look like it only goes around once.
We also saw a pattern appear in the shape left between lines. We noticed that however many dots there were, the shape in the middle would be a shape with that number of sides. This is true if the lines are created with any number of jumps (except that number itself which creates no lines).

Matthew from Primrose Lane Primary School noticed that:
One hits all numbers because if you move one it is bound to connect with every dot.
Pippa and Sophie from The Mount School York in the UK tried out different numbers of dots. Here is some of their work:
Circle of 8 dots
You can move around in steps of 1, 3, 5, 7
Circle of 9 dots
You can move around in steps of 1, 2, 4, 5, 7, 8
Circle of 10 dots
You can move around in steps of 1, 3, 7, 9
Click here to see a table containing Pippa and Sophie's work for 3 to 24 points.
Harvey from St Nicholas in the UK described a method for finding which step sizes will not visit all of the points:
To find it out, if the number of points is divisible by the amount you will skip, then you will not visit all the points. If we take 9 for example, and skip 3, then you will have 3 lines because 3$\times$3 = 9.
Mahdi from Mahatma Gandhi International School in India added:
My initial observations was that when you choose a step size that isn’t a factor of the number of points chosen, then we might achieve the result of striking all points. But soon, with multiple trials, I found out that for example, even though 4 is not a factor of 10, all points are not visited!? Something was off, but I couldn’t figure out why...
GG and Avirat from Wilson's Grammar School in the UK, Ivan, Jasmine and Lavender from Harrow International School HK in Hong Kong, Matthew, Pippa and Sophie and Mahdi described which step sizes will not visit all of the points. Matthew wrote:
Any factor of the number of dots fails to connect with all the dots. Also any multiple of the factor fails to hit.
Pat from Rugby School Thailand used algebraic notation and language to say the same thing (GCD = greatest common divisor = highest common factor = HCF):
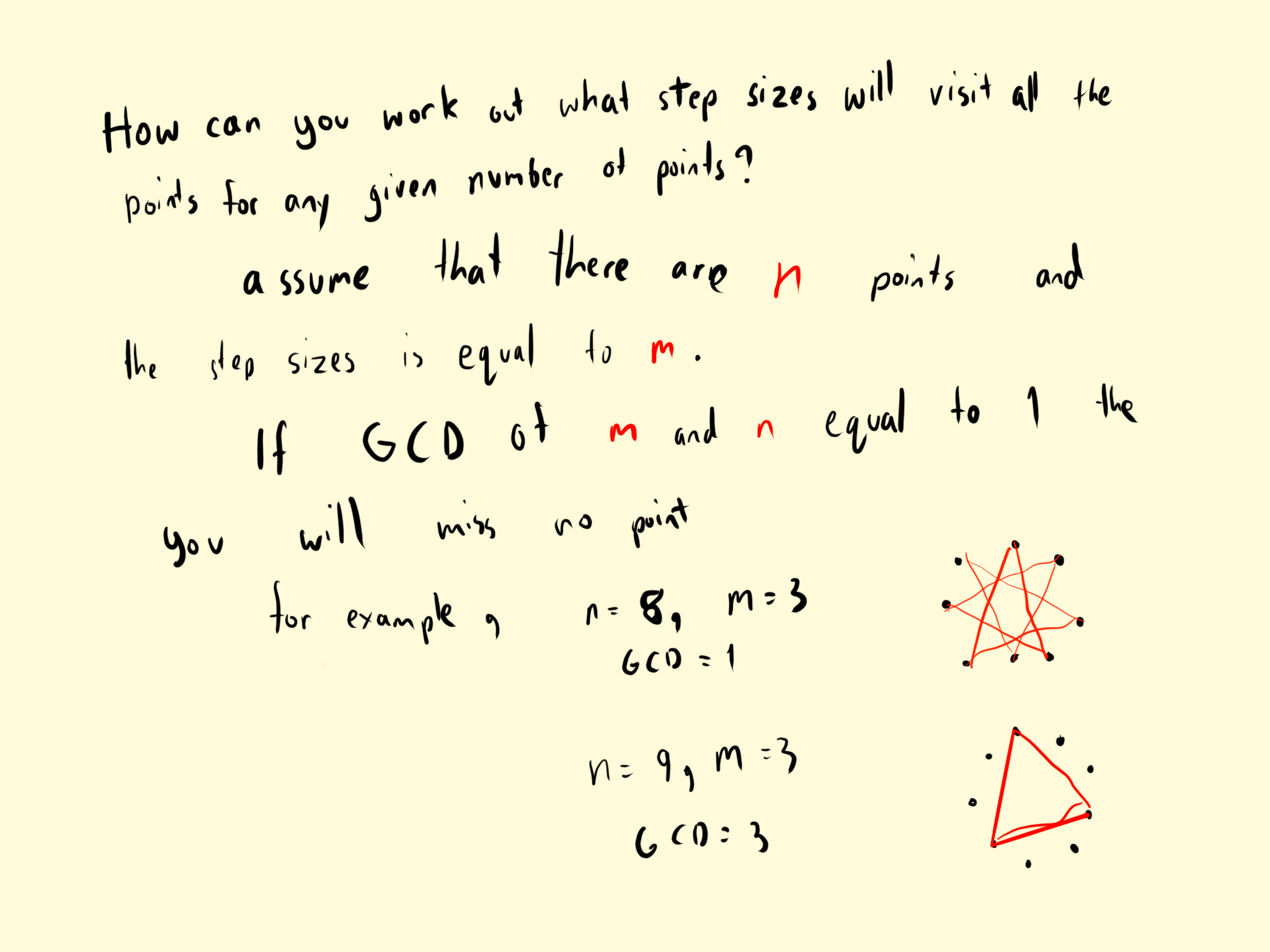
Han Chin from Hong Kong and Mahdi explained why this happens. This is Han Chin's work (Han Chin says two numbers are relatively prime if their GCD is 1):


Now consider $5$ points. You can visit all the points irrespective of the step size. Which other numbers have this property?
Bethan from Temple Newsom Halton Primary School wrote:
I have found that if the number of points in this problem is a prime number then all of the steps work and all of the steps join each other together whereas if the number of points is not a prime number then not all of the step [sizes] work and not all of them join each other together. I have proved this by testing my theory on different numbers of points that are prime and not prime. For example 23 is a prime number and all of its steps work whereas 21 is not a prime number and therefore not all of the steps on it work. We have also tried this with 3 points 11 points and 13 points. My theory works on all of these.
Pippa and Sophie, Matthew, Harvey and Han Chin linked this to their ideas about factors and relatively prime numbers. Matthew wrote:
Any time you have a prime number of dots, all the dots will be connected because it has no factors to miss.
Han Chin wrote that [this] is because a prime number is relatively prime to all the numbers smaller than it.
Can you find a relationship between the number of dots on the circle and the number of step sizes that will ensure that all points are hit?
Pippa and Sophie recorded the number of step sizes that hit all the points for 3 to 24 points and made some observations:

Click here to see the whole table.
If the number of points is prime the formula for the number of step sizes is $n-1$ where $n$ is the number of points.
All the step sizes are even.
Mahdi linked this to Euler's Totient Function. See this problem to learn more about Euler's Totient Function. This is Mahdi's work:
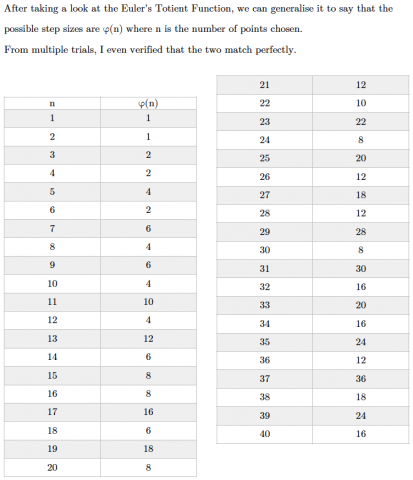

Teachers' Resources
Why do this problem?
This problem encourages students to see the maths underpinning a situation. In this case it is the importance of factors and multiples in what is at first glance a geometrical setting.
To avoid spoiling the surprise, it may be worth doing this activity at the start of work on the topic, without telling the students what the topic is...
Possible approach
You will find sheets of different dot-circles for printing out at the bottom of the problem page.
Ask students to draw a five pointed star starting and ending at one of the "points" or vertices of the star. They must do this without taking their pencil off the paper and without drawing over a line they have already drawn. Many learners will have met this before.
Ask the group to discuss in pairs a description of what they did that they can share with the rest of the group. "How would you explain to someone else, at the other end of a phone, how to draw the star?"
Look out for ideas such as step size and ways to describe positions.
When ready, demonstrate a five pointed star with the interactivity and discuss the notation that has been used (going anticlockwise, stepping by two leaves two gaps between the points on the circle). Alternatively, you might get a group of students to stand in a circle and make the stars with string (by passing a ball of string).
Discuss points of interest including:
- What happens if you move clockwise.
- What constitutes a star (in these notes a polygon created from a step size of 1 is not a star).
- There is only one star on a five-dot circle.
- Complementary step sizes produce the same star (step size two is equivalent to step size three in this five-dot context)
Ask students to make as many stars as possible on a seven-dot circle:
- How many stars can they make?
- How do they know they have them all?
Students can now focus on generalising their results for any dot-circle.
Key questions
- What are the things that affect the number of stars you can draw?
- Can you find one rule to determine the number of stars or do you need different rules for different circumstances?
- Can you write a rule, or set of rules, that someone who had never seen the problem, could understand?
Possible support
Possible extension
