Flipping Twisty Matrices
Problem
One of the ways to work with transformations is to use a matrix. If you have not met matrices before you might like to start by looking at the problem The Matrix.
Here is a reminder of how matrix multiplication works for a $2 \times 2$ matrix and a $2$D vector:
$$ \begin{pmatrix}a&b\\c&d\end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix} =\begin{pmatrix}ax+by\\cx+dy\end{pmatrix} $$
If the matrix $\begin{pmatrix}a&b\\c&d\end{pmatrix}$ represents a transformation in the $x,y$ plane, then we can find the image of a point with coordinates $(p, q)$ by multiplying the transformation matrix and the position vector of the original point:
$$\begin{pmatrix}a&b\\c&d\end{pmatrix} \begin{pmatrix}p\\q\end{pmatrix}$$
Example: Consider the transformation represented by the matrix $\begin{pmatrix}1&2\\0&1\end{pmatrix}$. By considering the image of the points $(0,0)$, $(1, 0)$, $(0, 1)$ and $(1, 1)$ describe what this transformation does to the unit square.
$\begin{pmatrix}1&2\\0&1\end{pmatrix}\begin{pmatrix}0\\0\end{pmatrix}=\begin{pmatrix}0\\0 \end{pmatrix}$
$\begin{pmatrix}1&2\\0&1\end{pmatrix}\begin{pmatrix}1\\0\end{pmatrix}=\begin{pmatrix}1\\0\end{pmatrix}$
$\begin{pmatrix}1&2\\0&1\end{pmatrix}\begin{pmatrix}0\\1\end{pmatrix}=\begin{pmatrix}2\\1\end{pmatrix}$
$\begin{pmatrix}1&2\\0&1\end{pmatrix}\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}3\\1\end{pmatrix}$
So the unit square is transformed into a parallelogram (this type of transformation is called a shear).
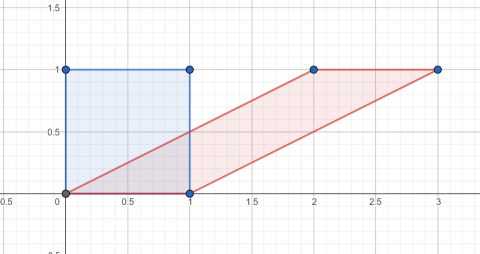
You can find the image of the square in a single matrix multiplication as shown below:
$\begin{pmatrix}1&2\\0&1\end{pmatrix}\begin{pmatrix}0 & 0 & 1 & 1\\0 & 1 & 1 & 0\end{pmatrix}=\begin{pmatrix}0& 2& 3&1\\0 & 1 &1&0 \end{pmatrix}$
In this case I have listed the four vertices of the unit square in clockwise order, starting at $(0,0)$.
Now consider matrices of the form
$$\begin{pmatrix}a&0\\0&d\end{pmatrix} $$
where $a$ and $d$ each take either the value $1$ or the value $-1$ (so there are four different matrices).
Explore what these four different transformations do. It would be a good idea to try different shapes, such as a square and a trapezium, for example the one with coordinates $(1,0)$, $(3, 0)$, $(2, 1)$ and $(0,1)$, so that you can tell whether a shape is reflected or rotated.
What happens if we consider instead matrices of the form $\begin{pmatrix}0&b\\c&0\end{pmatrix} $ where $b$ and $c$ can take the values $1$ and $-1$?
What if any of $a$, $b$, $c$ and $d$ can be equal to $1$, $-1$ or $0$?
What happens to the areas of the shapes under the different transformations?
You might like to use this Matrix Transformation tool to help test out your ideas.
There are more matrix problems in this feature.
Getting Started
Student Solutions
Yiran from Guanghua Qidi in China chose a shape and looked at its image under matrices of the form $ \left( \begin{array}{cc} 0 & b \\ c & 0 \end{array} \right) $ where $b$ and $c$ can take the values $1$ and $-1.$ This is Yiran's work (click on the image to open a larger version). Note that for $b=1, c=-1$ the rotation is actually clockwise,
not anticlockwise - as shown in Yiran's diagram.
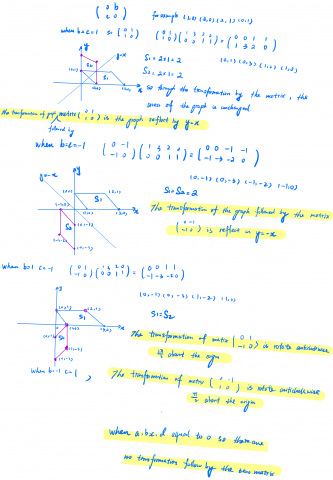
Andrei from School No. 205, Bucharest, Romania considered matrices of the form $ \left( \begin{array}{cc} a & 0 \\ 0 & d \end{array} \right) $ where $a$ and $d$ can take the values $1$ and $-1.$ Andrei also looked at more general points under both families of matrices. This is Andrei's work:
1. $b = c = 0,\ a = d = -1$ $$ \left( \begin{array}{cc} -1 & 0 \\ 0 & -1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} -x \\ -y \end{array} \right) .$$ This means each point (x, y) transforms into its symmetrical image with respect to the origin, i.e. into the point (-x, -y). This is a rotation of
180 degrees about the origin.
2. $b = c = 0,\ a = - 1,\ d = 1$ $$ \left( \begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} -x \\ y \end{array} \right) .$$ Here, it is a reflection in the y-axis.
3. $b = c = 0,\ a = d = 1$ $$ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} x \\ y \end{array} \right) .$$ In this situation each point transforms into itself.
4. $b = c = 0,\ a = 1,\ d = -1$ $$ \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} x \\ -y \end{array} \right) .$$ This transformation leaves the abscissa unchanged and modifies the sign of the ordinate, being a reflection in the x-axis.
Now, I look at the next set of transformations.
5. $a = d = 0,\ b = c = 1$ $$ \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} y \\ x \end{array} \right) .$$ In this transformation, the abscissa and the ordinate are interchanged, the transformation being a reflection in respect to the line $y=x$, the angle
bisector of the first quadrant.
6. $a = d = 0,\ b = 1,\ c = -1$ $$ \left( \begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} y \\ -x \end{array} \right) .$$
Andrei also concluded that this is a rotation of $90^\circ$ clockwise about the origin.
7. $a = d = 0,\ b = c = -1$ $$ \left( \begin{array}{cc} 0 & -1 \\ -1 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} -y \\ -x \end{array} \right) .$$ This corresponds to a reflection in the line $y=-x$.
8. $a = d = 0,\ b = -1,\ c = 1$ $$ \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} -y \\ x \end{array} \right) .$$ This corresponds to a rotation of the point by 90 degrees anti-clockwise about the origin.
Teachers' Resources
This problem introduces the idea of how matrices can be used to represent 2D transformations. Students are then asked to consider $2 \times 2$ matrices with entries of $1$, $-1$ or $0$ and see what transformations these represent.
Students might like to use this Matrix Transformation tool to help them investigate the problem. In this tool the four corners of a quadrilateral are given as a $2 \times 4$ matrix, where the coordinates appear as the columns of the matrix, in clockwise (or anticlockwise) order. Students might like to start by changing some numbers in the matrices to see what the two matrices do.
Students can also be asked to think why the problem suggests that they consider what the matrices do to both a square and a another shape - why might considering what happens to a square not be enough?
The Matrix Transformation tool can also be used to test out students ideas as a whole class.
There are more matrix problems in this feature. The problem Square Pair follows on from this problem and considers more general 2D transformations.