A Shade Crossed
Find the area of the shaded region created by the two overlapping triangles in terms of a and b?
Problem
| Find the area of the shaded region in terms of $a$ and $b$? | Image
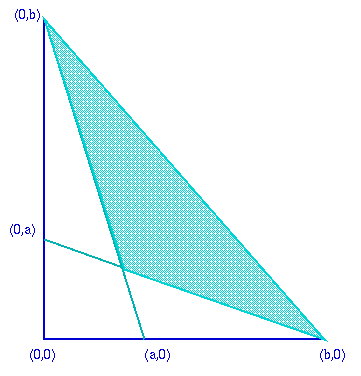
|
Student Solutions
There were two solutions from Madras College, one from Thomas, James, Mike and Euan and the other from Sue Liu which is reproduced below.
Image
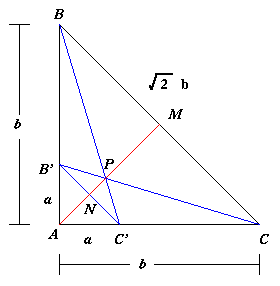
| This triangle is a right angled isosceles triangle, the hypotenuse being $\sqrt{2}b$. We draw a line through $A$ and point $M$, the midpoint of the line $BC$. We draw the line $B'C'$ giving another right angles isosceles triangle $AB'C'$, similar to triangle $ABC$ but with sides a and hypotenuse $\sqrt{2}a$. Now $N$ is the point where the line $B'C'$ meets the line $AM$, and $P$ is the point where $BC'$ meets $B'C$ (also on $AM$).
It is clear that triangle $PBC$ is similar to triangle $P B'C'$ and the enlargement factor from $B'C'$ to $BC$ is $b/a$. So the line $PM$ is $b/a$ times as long as the line $PN$. Also the line $AN$ is half the length of $B'C'$, so it is $\sqrt{2}a/2$. The line $AM$ is half the length of $BC$ so it is $\sqrt{2}b/2$. |
If we let $PN$ be $x$ then we have an equation:
$$x + \frac{bx}{a} + \frac{\sqrt{2}}{2}a = \frac{\sqrt{2}}{2}b$$
Solving this equation gives $$x = {\frac{\sqrt{2}}{2}}{\frac{(b - a)a}{(a + b)}}$$
$PM$ is the height of the shaded triangle and $PM = xb/a$.
Area of the shaded triangle is:
$$\frac{xb}{a} \cdot \frac{\sqrt{2}}{2} \cdot b = \frac{b^{2}(b - a)}{2(b + a)}$$
