Frosty the Snowman

Well done to the students who submitted solutions to this challenging problem: Walter from Abingdon School, and Nina and Jokubas from London Academy of Excellence Tottenham, in the UK.

Nina, Jokubas and Walter sent in solutions that involved the radii as linear functions of time, i.e. $r_1=kt_2r$ and $r_2=kt+3R$ (where $k<0$). As Jokubas argued, using S.A. to stand for surface area

$\dfrac{d}{dt}V \propto \text{S.A.}$ 

Therefore $\dfrac{d}{dt}V = - k \text{S.A.}$  

$\dfrac{d}{dt}\left( \dfrac{3}{4} \pi r^3\right) = -k (4\pi r^2)$ 

Then dividing both sides by $4\pi r^2$ leads to 

$\dfrac{dr}{dt}=-k$.

$\int -k dt$ (Integrating $\dfrac{dr}{dt}$ gives us a function of $r$ in terms of $t$ (and $k$).)

$\text{Radius} =-kt +C$  

Which Jokubas used to obtain $R_T=-kt+2r$ and $R_B=-kt+3r$. (Note that $r$ is used here instead of the $R$ in the question for the intial radius).

(Note that including a negative sign is a common choice when you know that something is decreasing, but this means that $k$ must be positive to ensure that $-k$ is negative.)

Walter's work here shows how these were obtained using a slightly different method that used the chain rule, and goes on to give a full solution to the first part of the problem (click here to see a larger version):

Image

Image

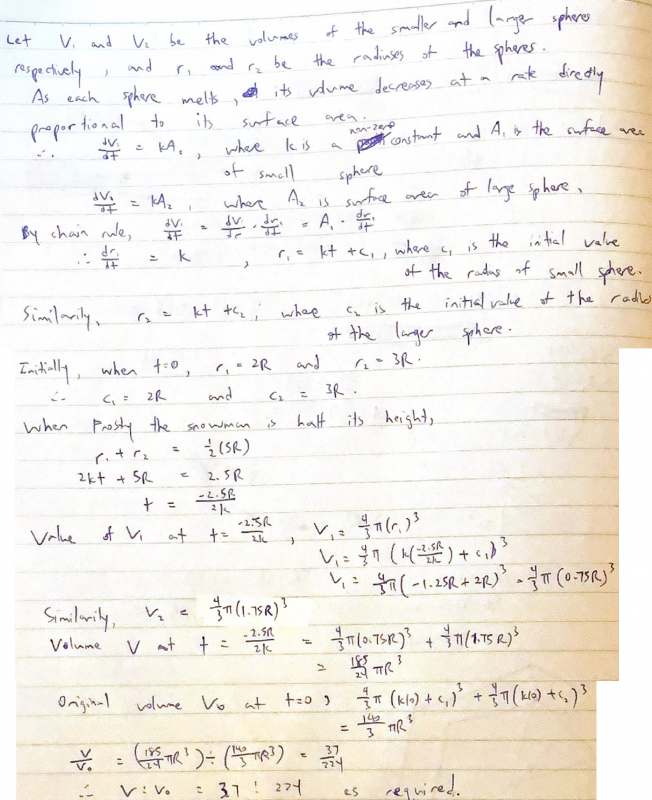
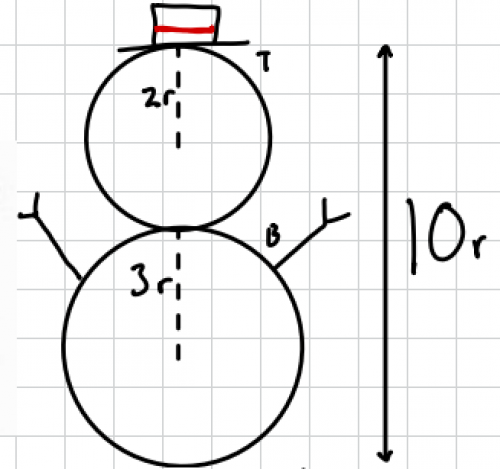
You may have noticed a slight error here involving the initial height (which other students also made). 

If the two snowballs initially have radii $2R$ and $3R$ then Frosty's initial height is not $5R$, as Jokubus' diagram helpfully shows here. 

You might find it interesting to think about why the slight error here hasn't affected the final result. 

Walter's solution to the second part of the problem is almost perfect (click here to see a larger version):

Image

Once Walter realises that the top snowball is completely melted (and has a negative radius), Walter removes that snowball from the volume calculation - which is correct.

However, Walter should have recalculated the appropriate radius of the remaining snowball using the new information that the smaller snowball had disappeared.

What should the answer be?

At the end of the problem we asked you about what assumptions you had used and whether you think these are realistic. Nina made the following comments:

Assumption is uniform melting and constant proportionality. Real snow would melt unevenly. To be more realistic, consider varying melting rates based on temperature.

This is an interesting variation of the problem - you could think about how you might start to model varying melting rates.