Classifying solids using angle deficiency
Problem
Like most NRICH articles the reader will get most from it by doing the mathematics before moving on from one paragraph to the next.
(This article is based on a mathematics workshop for 12 year olds given by Warwick Evans and Alison Clark Jeavons in Cambridge in February 2000. The photos were taken at the ATE / NRICH Mathematics Superweek holiday for 10 to 13 year olds at Southam in August 2000. )
In this article we shall find out why there are only five regular polyhedra, that is solids where all the faces are regular polygons (triangles, squares, pentagons and hexagons). A shape is called 'regular' when all the sides are the same length, all the angles are the same, all the faces are the same and the pattern in which the faces meet at each vertex (the vertex form) is the same. We shall also explore the properties of the semi-regular polyhedra, the solids where the faces are two or more different regular polygons coming together in the same pattern at each vertex.
In the pictures Ellie is holding a dodecahedron which is one of the five regular polyhedra and Vicky is holding a great rhombicosidodecahedron which is a semi-regular polyhedron with square, hexagonal and octagonal faces.

All you need to follow this article is very simple arithmetic, to know what an angles is and to use simple logical thinking. Though it is not essential you will be able to visualise the solids much more easily if you can use a construction kit (such as the plastic shapes which fit together made by Polydron as shown in the photos) to make the solids while reading this article.
The regular polyhedra are called the Platonic solids and the semi-regular ones the Archimedean solids after two famous Greek mathematicians. 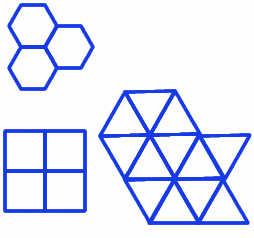
Using the plastic polygons made by Polydron, we can discover the three regular tessellations made by triangles, squares and hexagons.
Next we can introduce a notation to describe the vertex formed by each tessellation. This notation, describing the number of edges of each polygon meeting at a vertex of a regular or semi-regular tessellation or solid, was devised by the Swiss mathematician Ludwig Schlafli (1814-1895). He was a schoolteacher who did mathematical research in his spare time.
Each vertex in the hexagonal tessellation is surrounded by three 6-sided polygons and we say that the vertex form is 666.
The square tessellation has vertex form 4444.
In a similar way, each of the vertices in the triangular tessellation is surrounded by six 3-sided polygons and has the vertex form 333333. The interior angles of the triangle, square and hexagon are $60^{\circ}$, $90^{\circ}$ and $120^{\circ}$ respectively and it can be seen that the sum of the angles at a vertex in any of the three tessellations is $360^{\circ}$. We can see that these are the only possible regular plane tessellations because pentagons, with interior angles of $108^{\circ}$, cannot fit together around a vertex and for polygons with more than six sides the interior angles are more than $120^{\circ}$ so it is impossible to fit three or more together around a vertex.
In any solid, the number of faces at a vertex must be more than two. We begin with triangles.
Using only triangles, each vertex must have fewer than 6 faces at a vertex (otherwise we end up with a plane tessellation). We can join three 3-gons (i.e. triangles) to make a vertex with vertex form 333. Carry on constructing a solid so that each vertex has form 333 and we arrive at the tetrahedron with 4 triangular faces.
We can join four 3-gons to make a vertex with vertex form 3333 and this solid is the octahedron with 8 triangular faces.
We can join five 3-gons (i.e. triangles) to make a vertex with form 33333 and this solid is the icosahedron with 20 triangular faces.
Now move on to squares. To make a solid, we must have more than 2 faces at a vertex and fewer than 4 [Why fewer than 4?]. This leaves us with the vertex form 444 and we construct the cube (or hexahedron) with 6 square faces.
Next comes the pentagon. Each vertex of any solid must have more than 2 faces. Once you convince yourself that we cannot have a vertex of form 5555 we are left with the regular solid with vertex form 555 called the dodecahedron with 12 pentagonal faces.
We cannot make a regular solid with any polygon with six or more sides [Why?].

| Name | Vertex Form | n(Faces) = F | n(Vertices) = V | n(Edges)=E | Angle Deficiency | Total Angle Deficiency |
|---|---|---|---|---|---|---|
| Tetrahedron | 333 | 4 | ||||
| Octahedron | 3333 | 8 | ||||
| Icosahedron | 33333 | 20 | ||||
| Cube | 444 | 6 | ||||
| Dodecahedron | 555 | 12 |
After careful counting of vertices and edges - it isn't as easy as it sounds - we can complete the next two columns. Try to do this for yourself then check your results .
The conjecture that F + V - E = 2 should come from examining the numbers in the F, V and E columns. This is the famous (and so useful) Euler's Theorem . Here it is only a conjecture made from looking at our table but it is in fact true - finding a proof is left to the reader.
The next column - Angle Deficiency - supplies the core theme of this activity.
Consider the tetrahedron. Its vertex form is 333 and so the sum of the angles at each of its vertices is $60^{\circ}+60^{\circ}+60^{\circ}=180 ^{\circ}$ and we say that the angle deficiency is $360^{\circ}-180^{\circ}$ that is $180^{\circ}$. It is what you get if you flatten the polyhedron at a vertex and measure the missing angle.
Can you see that the angle sum at the vertex of any solid is bound to be less than $360^{\circ}$? [Why?]
Definition: The angle deficiency at a vertex is $360^{\circ}$ minus (the angle sum at the vertex).
We can fill in the next column in the table with the angle deficiency for each Platonic solid provided we know the interior angle of each $n$-gon.
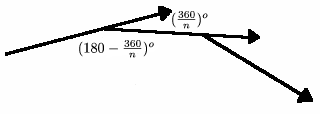
A little diversion here takes us back to the plane, it links ideas of angle deficiency with curvature and it proves the formula for the interior angle of a regular $n$-gon which is $(180-360/n)^{\circ}$. From this formula we see that the interior angles of 3-, 4-, and 5-gons are 60$^{\circ}$, 90$^{\circ}$ and 108$^{\circ}$ respectively.
If you walk all the way around a circle back to your starting point you turn through a total angle of $360^{\circ}$ or (using another measure) $2\pi$ radians. Imagine walking around a regular $n$-gon starting from one of the vertices. Now the curvature, instead of being evenly spread around the edge, is concentrated at the vertices. At each vertex you make the same turn to walk along the next edge. When you get back to your starting point you turn through the same angle to face the direction you were facing at the start and altogether you have turned through a total angle of $360^{\circ}$. Each of these turns is therefore $(360/n)^{\circ}$, the exterior angle at the vertex. The interior angle is therefore $(180-360/n)^{\circ}$.
The final column in the table - total angle deficiency - is just the sum of the angle deficiencies at every vertex of a particular solid. Since, in each case, the vertex form is the same at each vertex, we can just multiply the number of vertices (column V) by the angle deficiency we have just calculated. We end up with the following table.
| Name | Vertex Form | n(Faces) = F | n(Vertices) = V | n(Edges)=E | Angle Deficiency | Total Angle Deficiency |
|---|---|---|---|---|---|---|
| Tetrahedron | 333 | 4 | 4 | 6 | 180 | 720 |
| Octahedron | 3333 | 8 | 6 | 12 | 120 | 720 |
| Icosahedron | 33333 | 20 | 12 | 30 | 60 | 720 |
| Cube | 444 | 6 | 8 | 12 | 90 | 720 |
| Dodecahedron | 555 | 12 | 20 | 30 | 36 | 720 |
We have ended up with the result that the total angle deficiency for each of the five Platonic Solids is $720^{\circ}$. But is the result generally true? Is the total angle deficiency for any solid $720^{\circ}$? Well, yes it is and you can take it `on trust' for now - but you had better check it with some other solids and you might like to seek a proof on the internet or in a book. We are
generalising ideas from two dimensions (the plane) to three dimensions. In the plane the sum of the exterior angles of any polygon is always $360^{\circ}$ (or $2\pi$ radians); this is linked to the concept of curvature and the fact that, in the limit as $n$ tends to infinity, we get a circle of length $2\pi$ times its radius. In the plane the constant $360^{\circ}$ or $2\pi$ radians plays the
same role as the total angle deficiency plays in 3-D. The total angle deficiency for any solid is $720^{\circ}$ or $4\pi$ radians. This is linked to the concept of curvature and the fact that, in the limit as $n$ tends to infinity, we get a sphere with surface area of $4\pi$ times the square of its radius.
Now let us relax the condition of regularity. A semi-regular solid is one which is made up of more than one type of polygon but in which all vertices have the same vertex form.
Suppose we choose the vertex form 366 so that each vertex is surrounded by one 3-gon and two 6-gons. Will this choice generate a semi-regular solid and, if so, how many hexagons and how many triangles do we need? We aim to use Euler's theorem and the Total Angle Deficiency theorem to help us fill in another row in our table. We already have the second and the last columns.
| Name | Vertex Form | n(Faces) = F | n(Vertices) = V | n(Edges)=E | Angle Deficiency | Total Angle Deficiency |
|---|---|---|---|---|---|---|
| 366 | 720 |
Now we go through the following steps:
- angle deficiency - since the vertex form is 366, the angle deficiency must be $360^{\circ}-300^{\circ}=60^{\circ}$
- number of vertices - since all vertices have the same form, we can divide 720 by 60 to get the number of vertices which is 12
- number of edges - since each vertex is surrounded by 3 faces (and therefore by 3 edges too) we can argue that the number of edges counted is 12 x 3 = 36 but in doing so we have counted the edges twice, [why? well once at each end] so the number of edges must be half of 36, that is 18
- number of faces - use Euler's Theorem F + V - E = 2 to get F = 8
| Name | Vertex Form | n(Faces) = F | n(Vertices) = V | n(Edges)=E | Angle Deficiency | Total Angle Deficiency |
|---|---|---|---|---|---|---|
| 366 | 8 | 12 | 18 | 60 | 720 |
But how many of the 8 faces are triangles and how many are hexagons? What is the shape called?
Count the triangles first. Since each vertex has one 3-gon and there are 12 vertices, we can argue that the number of triangles must be $12\times 1= 12$ but in doing so we have counted each triangle 3 times over, once at each of its vertices since each triangle has 3 vertices. So the number of triangles must be $12/3=4$.
Count the hexagons next. We could just say $8-4=4$ but let's double check. Since each vertex has two 6-gons and there are 12 vertices, we can argue that the number of hexagons must be $12\times 2=24$ but in doing so we have counted the number of hexagons 6 times since each hexagon has 6 vertices. So the number of hexagons must be $24/6=4$.
| Name | Vertex Form | n(Faces) = F | n(Vertices) = V | n(Edges)=E | Angle Deficiency | Total Angle Deficiency |
|---|---|---|---|---|---|---|
| Truncated Tetrahedron | 663 |
4 3-gons
4 6-gons
|
12 | 18 | 60 | 720 |

Why not just choose a possible vertex form, and see what happens? Your vertex form must be such that the angle sum is less than $360^{\circ}$. Things may go wrong. For example, if you were to choose the vertex form 335 then the angle deficiency is $360-120-108=132$ which does not divide 720 so no semi-regular solid with such a vertex form exists.
Some vertex forms produce prisms, such as 344 the triangular prism which has three square faces and two triangular faces. Other vertex forms produce anti-prisms. In addition to the prisms and anti-prisms you will produce all the Archimedean solids (named after Archimedes) whose details are on the completed table below. You may like to fill in your own table and then check your results with this table at the end of this article.

Duncan and Suzanne have each made a rhombicuboctahedron with vertex form 3444. By using 'skeleton' pieces for the faces rather than solid plastic polygons you can look inside the polyhedra to study them.


The first known mention of the thirteen "Archimedean solids" is in a manuscript from the fifth book of the "Collection" of the Greek mathematician Pappus of Alexandria, who lived in the beginning of the fourth century AD.
You will find illustrations of the polyhedral solids and much interesting information about these solids and their geometrical and practical construction on the World Wide Web site maintained by Tom Gettys and further information at http://mathworld.wolfram.com/ArchimedeanSolid.html
The St Andrew's web site is a good starting point for finding more about Plato . and about Archimedes .
The 5 Platonic and 13 Archimedean Solids
| Name of Solid | Vertex Form | Number of Faces | Number of Vertices | Number of Edges | Angle Deficiency | Total Angle Deficiency |
|---|---|---|---|---|---|---|
| Tetrahedron | 3 3 3 | 4 | 4 | 6 | 180 | 720 |
| Cube | 4 4 4 | 6 | 8 | 12 | 90 | 720 |
| Octahedron | 3 3 3 3 | 8 | 6 | 12 | 120 | 720 |
| Dodecahedron | 5 5 5 | 12 | 20 | 30 | 36 | 720 |
| Icosahedron | 3 3 3 3 3 | 20 | 12 | 30 | 60 | 720 |
| Truncated Tetrahedron | 3 6 6 | 8=4+4 | 12 | 18 | 60 | 720 |
| Truncated Cube | 3 8 8 | 14=8+6 | 24 | 36 | 30 | 720 |
| Truncated Octahedron | 4 6 6 | 14=6+8 | 24 | 36 | 30 | 720 |
| Truncated Dodecahedron | 3 10 10 | 32=20+12 | 60 | 90 | 12 | 720 |
| Truncated Icosahedron | 5 6 6 | 32=12+20 | 60 | 90 | 12 | 720 |
| Cuboctahedron | 3 4 3 4 | 14=8+6 | 12 | 24 | 60 | 720 |
| Icosidodecahedron | 3 5 3 5 | 32=20+12 | 30 | 60 | 24 | 720 |
| Snub Dodecahedron | 3 3 3 3 5 | 92=80+12 | 60 | 150 | 12 | 720 |
| Rhombicuboctahedron | 3 4 4 4 | 26=8+18 | 24 | 48 | 30 | 720 |
| Great Rhombicosidodecahedron | 4 6 10 | 62=30+20+12 | 120 | 180 | 6 | 720 |
| Rhombicosidodecahedron | 3 4 5 4 | 62=20+30+12 | 60 | 120 | 12 | 720 |
| Great Rhombicuboctahedron | 6 4 8 | 26=8+12+6 | 48 | 72 | 15 | 720 |
| Snub Cube | 3 3 3 3 4 | 38=32+6 | 24 | 60 | 30 | 720 |

Sadly Warwick died in July 2000. He was much loved by his colleagues and students as an inspiring teacher with original ideas and a wonderful way of helping people to understand and to enjoy mathematics. He had a great zest for life.
Teachers' Resources
This article takes you through the classification of the Platonic (regular) and Archimedean (semi-regular) solids, to find all of them and prove that there are no more.
I found it difficult to make a choice of article for the NRICH Tenth Anniversary Celebration. I chose this one because it has been the basis of so many enjoyable sessions that I have had both with young learners and also with teachers.
With any age group, from 10 upwards, I find the best approach is to explain the Schlafli code and demonstrate it with an actual Archimedean solid,and then to give individuals different codes with the task of making their solid for that code. According to how much time you have, and how much your group already know, you can structure the session so that they discover the Euler Relation and/or the total Angle Deficiency, you can arrive at a proof that there are only 5 Platonic Solids and you can fill in the tables for all the Archimedean Solids deducing the number of each shape of face as described in the article. There are many possibilities.
In the ATE Maths Superweek where the photos were taken we had a great Holiday Director called Ian Johnston and a very good cook called Mrs Higgins and the children never knew that these were one and the same person. Just before lunch on the morning we spent on this topic Ian (an engineer) joined us and the children, having decided to test him, excitedly showed him their models "Ian look at mine, it's a 466" , "Ian mine is a 3434, can you explain that?" ... and so on. It did not take long for Ian (an engineer) to work it out and the children were impressed.
Perhaps your class can make the models out of card and hang them from the ceiling.
