Another Triangle in a Triangle
Can you work out the fraction of the original triangle that is covered by the green triangle?
Problem
In the diagram below, points have been chosen that are one third of the way along each side. Each of these points is then joined to the opposite vertex.
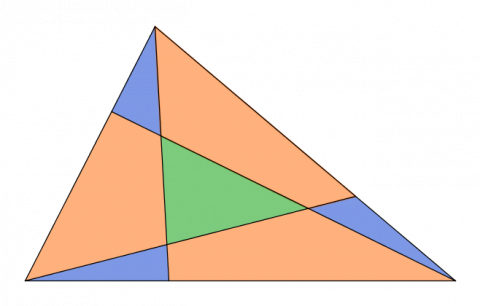
What fraction of the area of the whole triangle is the area of the green triangle?
If you are not sure how to get started, click below to read some thoughts, hints and suggestions that might be helpful. Before moving onto the next hint, do as much as you can with the information you have already worked out.
The base of triangle $a+f+e$ is $\tfrac{1}{3}$ of the base of the whole triangle.
Can you use this to work out the area of $a+f+e$ as a fraction of the whole triangle?
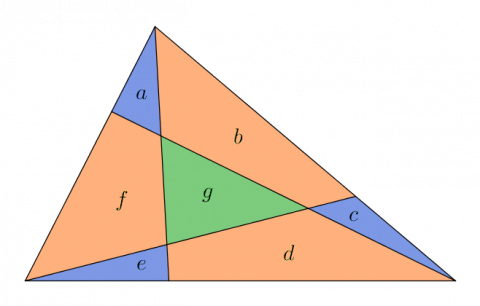
What about $a+b+c$ and $c+d+e$?
But none of these tell us anything about $g$.
But we do know that $a$, $b$, $c$, $d$, $e$, $f$ and $g$ together make the whole triangle!
Can we combine all this to find an expression for $g$ in terms of other areas?
It would be useful to know the areas of the little blue triangles...
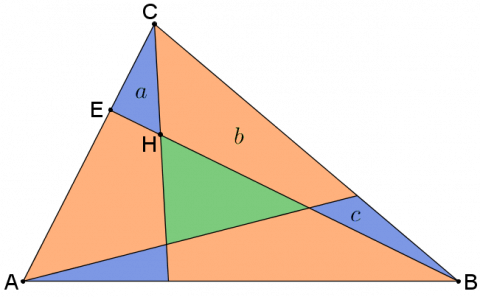
We know that:
- $a$ has the same height as triangle $ECB$.
- Triangle $ECB$ is $\tfrac{1}{3}$ of the whole triangle
If we can find the length $EH$ as a fraction of $HB$, we could work out the area of the blue triangle...
Sometimes it helps to add in an extra line...
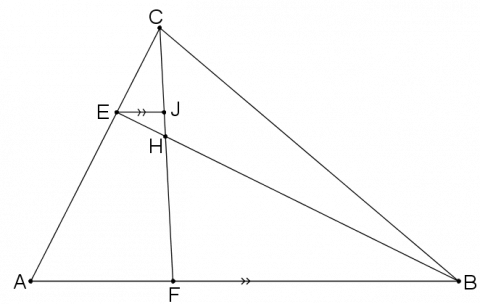
Can you find some similar triangles in this diagram?
How does $EJ$ compare with $AF$?
How does $EJ$ compare with $BF$
How does $EH$ compare with $HB$?
How does $EH$ compare with $EB$?
An alternative method for solving this problem is to use vectors.
Take a look at the Getting Started section if you want to think about this approach.
Extension
Can you find other interesting relationships in the diagram?
Can you prove that these relationships always hold?
With thanks to Dietmar Küchemann, whose ideas formed the basis of this problem.
Getting Started
An alternative approach is to use vectors.
In the diagram below, vectors $\bf{x}$ and $\bf{y}$ have been defined such that $\overrightarrow{AC}=3\bf{x}$ and $\overrightarrow{AB}=3\bf{y}$.
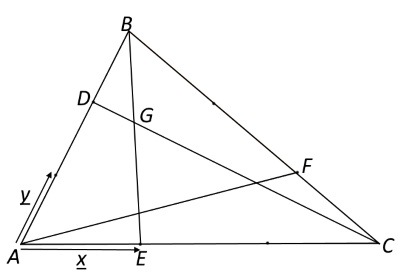
Click below for a series of hints to help you to work out the ratio of the length $DG$ to $DC$:
Can you express $\overrightarrow{DC}$ in terms of $\bf{x}$ and $\bf{y}$?
Can you express $\overrightarrow{BE}$in terms of $\bf{x}$ and $\bf{y}$?
By writing $\overrightarrow{DG}$ as $\lambda \overrightarrow{DC}$ and $\overrightarrow{BG}$ as $\mu \overrightarrow{BE}$, can you find two expressions for $\overrightarrow{AG}$?
By equating coefficients of $\bf{x}$ and $\bf{y}$, can you find $\lambda$?
Now you can use this information together with the first two hints in the problem to find the relationships between the areas.
Student Solutions
Sadaf from BSS in Pakistan found the relationship between then blue and green triangles:

$a+f+e$ to total $=1:3$
$a+b+c$ to total $=1:3$
$c+d+e$ to total $= 1:3$
using concept that ratio of areas of triangles with the same height is equal to ratio of their bases
(This idea can be seen in Triangle in a Triangle and in Areas and Ratios - breaking a triangle into two smaller triangles by dividing one of its sides in the ratio $a:b$, the areas of the two smaller triangles will also be in the ratio $a:b$)
Now three one thirds add up to a whole
$2a+b+2c+d+2e+f=$ one whole
this implies that
$a+c+e =g$
Reyna from Downside School used this same logic on many smaller triangles within the triangle. This is Reyna's work, with some additional diagrams added:
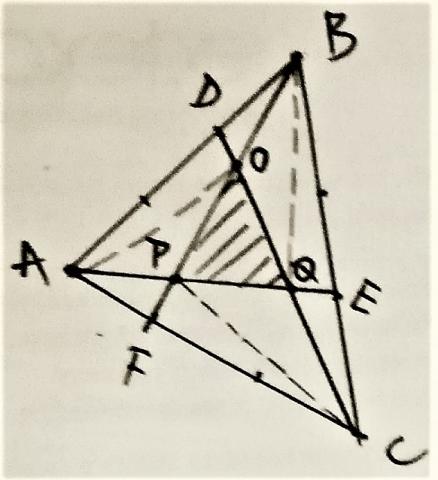
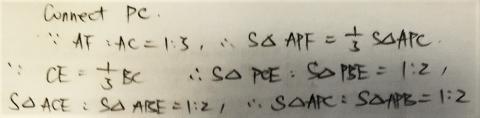
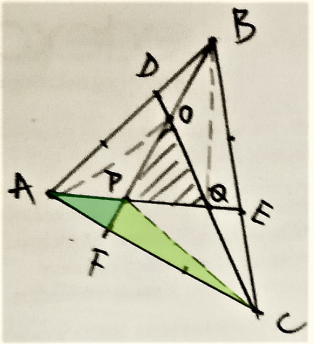
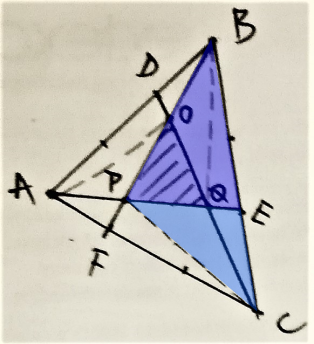
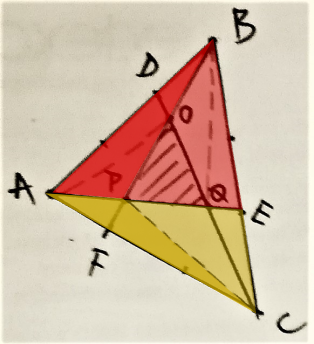
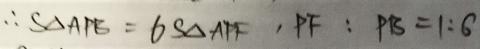

Jamie from Bournemouth School in the UK considered a more general case where each side is divided into $n$ sections. Jamie then used vectors to find the area of the green triangle in this general case, and then used $n=3$. This is Jamie's work:
Hoytem from Noodres college, Madras used coordinate geometry. This had a lot in common with Jamie's solution, but the coordinate geometry approach involves more algebra (even though Jamie was working in a more general case):
Attacking the problem with brute force will give results
Let the bottom left hand vertex of the largest triangle be $O$, the origin. Then, going anticlockwise around the triangle, let the other vertices be $A$ with coordinates $\left(a_x,0\right)$ then $B$ with coordinates $\left(b_x,b_y\right)$. Let $E$ be the point a third of the way along $BO$, with coordinates $\left(\frac23b_x, \frac23b_y\right)$, $D$ be the point on $OA$, with coordinates $\left(\frac13a_x,0\right)$ and $C$ be the point on $AB$, with coordinates $\left(\frac23a_x+\frac13b_x,\frac13b_y\right)$. These coordinates can be obtained by using the rules of similar triangles.
Finally, let the top vertex of the green triangle be $F$, with coordinates $\left(f_x,f_y\right)$ and, going clockwise around the triangle, let the other vertices be $G$, with coordinates $\left(g_x,g_y\right)$ then $H$, with coordinates $\left(h_x,h_y\right).$
In order to find the area of triangle, the following calculation can be done: $$A=\frac12(HF)(HG)\sin{F\hat{H}G}$$
First, the coordinates of $F$, $G$ and $H$ need to be found. (In terms of $a_x, b_x$ and $b_y$)
The equation of the line $BD$ is $$\frac{y-0}{x-\tfrac13a_x}=\frac{b_y-0}{b_x-\tfrac13a_x}\\
\Rightarrow y=\frac{3b_y}{3b_x-a_x}x-\frac{a_xb_y}{3b_x-a_x}$$
The equation of the line $EA$ is $$\frac{y-0}{x-a_x}=\frac{\tfrac{2}3b_y-0}{\tfrac23b_x-a_x}\\
\Rightarrow y=\frac{2b_y}{2b_x-3a_x}x-\frac{2a_xb_y}{2b_x-3a_x}$$
An equation can now be set up in $f_x$ (since the point $F$ is the intersection between the line $EA$ and the line $BD$): $$\begin{align}&\frac{3b_y}{3b_x-a_x}f_x-\frac{a_xb_y}{3b_x-a_x}=\frac{2b_y}{2b_x-3a_x}f_x-\frac{2a_xb_y}{2b_x-3a_x}\\
\Rightarrow & 3b_y\left(2b_x-3a_x\right)f_x-a_xb_y\left(2b_x-a_x\right)=2b_y\left(3b_x-a_x\right)f_x-2a_xb_y\left(3b_x-a_x\right)\\
\Rightarrow &\left(6b_xb_y-9a_xb_y\right)f_x-\left(6b_xb_y-2a_xb_y\right)f_x=a_xb_y\left(2b_x-3a_x\right)-2a_xb_y\left(3b_x-a_x\right)\\
\Rightarrow &\left(6b_xb_y-9a_xb_y-6b_xb_y+2a_xb_y\right)f_x=2a_xb_xb_y-3a_x^2b_y-6a_xb_xb_y+2a_x^2b_y\\
\Rightarrow&-7a_xb_yf_x=-a_xb_y\left(4b_x+a_x\right)\\
\Rightarrow &=f_x=\frac{a_x+4b_x}7\end{align}$$
We can now find $f_y$, since $\left(f_x,f_y\right)$ lies on the line $BD$ $$\begin{align}f_y&=\frac{3b_y}{3b_x-a_x}\left(f_x-\frac{a_x}3\right)\\
\Rightarrow f_y&=\frac{3b_y}{3b_x-a_x}\left(\frac{a_x+4b_x}7-\frac{a_x}3\right)\\
\Rightarrow f_y&=\frac{3b_y}{3b_x-a_x}\left(\frac{4\left(3b_x-a_x\right)}{21}\right)\\
\Rightarrow f_y&=\frac{4}{7}b_y\end{align}$$
The same process can be repeated to find the coordinates of $G$ and $H$, using the information that $G$ is the point of intersection between the lines $OC$ and $EA$ and $H$ is the point of intersection between the lines $OD$ and $BD$.
The equation of the line $OC$ is $$y=\frac{b_y}{2a_x+b_x}x$$
Using this information and the information above, the coordinates of $G$ are $$\left(\frac{4a_x+2b_x}7,\frac27b_y\right)$$
And the coordinates of $H$ are $$\left(\frac{2a_x+b_x}7,\frac17b_y\right)$$
Now, the length of $HF$ can be found. Let $HF_x=h_x-f_x$: $$\Rightarrow HF_x=\frac {2a_x+b_x-a_x-4b_x}{7}\\
\Rightarrow HF_x=\frac{a_x-3b_x}7$$
Similarly, let $HF_y=h_y-f_y$ $$\Rightarrow HF_y=\frac{b_y-4b_y}7\\
\Rightarrow HF_y=\frac{-3}{7}b_y\\
\begin{align} & HF=\sqrt{\left(HF_x\right)^2+\left(HF_y\right)^2}\\
\Rightarrow & HF = \frac{\sqrt{\left(a_x-3b_x\right)^2+\left(3b_y\right)^2}}7\\
\Rightarrow & HF = \frac{\sqrt{a_x^2-6a_xb_x+9b_x^2+9b_y^2}}7\end{align}$$
The length of $HG$ can be found in a similar way $$HG=\frac{\sqrt{4a_x^2+4a_xb_x+b_x^2+b_y^2}}7$$
Now, $\dfrac{(HF)(HG)}2$ needs to be found. After a lot of algebraic manipulation, $$\dfrac{(HF)(HG)}2=\frac{\sqrt{4a_x^4-20b_xa_x^3+\left(13b_x^2+37b_y^2\right)a_x^2+30b_x\left(b_x^2+b_y^2\right)a_x+9\left(b_x^2+b_y^2\right)^2}}{98}$$
Let $k=\sqrt{4a_x^4-20b_xa_x^3+\left(13b_x^2+37b_y^2\right)a_x^2+30b_x\left(b_x^2+b_y\right)^2a_x+9\left(b_x^2+b_y^2\right)^2}$
Then $\dfrac{(HF)(HG)}2=\dfrac{k}{98}$
Now, $F\hat{H}G$ needs to be found. The gradient of the line $BD$ is $\dfrac{3b_y}{3b_x-a_x}$, and the gradient of the line $OC$ is $\dfrac{b_y}{2a_x+b_x}$
From looking at a diagram of the triangles, it can be seen that $$F\hat{H}G=\arctan{\frac{3b_y}{3b_x-a_x}}-\arctan{\frac{b_y}{2a_x+b_x}}$$
Let $a=\arctan{\dfrac{3b_y}{3b_x-a_x}}\Rightarrow \tan a = \dfrac{3b_y}{3b_x-a_x}$ and $b=\arctan{\dfrac{b_y}{2a_x+b_x}}\Rightarrow \tan b = \dfrac{b_y}{2a_x+b_x}$
It is true that $\tan{(a-b)}=\dfrac{\tan a -\tan b}{1+\tan a \tan b}$
$$\Rightarrow a-b=F\hat{H}G=\arctan{ \left( \dfrac{ \left( \frac{3b_y}{3b_x-a_x} \right)-\left(\frac{b_y}{2a_x+b_x}\right) }{ 1+\left( \frac{3b_y}{3b_x-a_x} \right)\left(\frac{b_y}{2a_x+b_x}\right) } \right) }\\
\Rightarrow F\hat{H}G = \arctan{\frac{7a_xb_y}{5a_xb_x-2a_x^2+3b_x^2+3b_y^2}}$$
It is now required to find $\sin{F\hat{H}G}= \sin{ \arctan{\dfrac{7a_xb_y}{5a_xb_x-2a_x^2+3b_x^2+3b_y^2}}}$

It is easy to see, if a right angle triangle is drawn, in which, for an angle $\theta$ in the right angled triangle, if $\tan{\theta}=\frac ab$, then $\sin{\theta}=\sin{\arctan{\frac ab}}=\dfrac{a}{\sqrt{a^2+b^2}}$. Applying this logic, $$\sin{ \arctan{\dfrac{7a_xb_y}{5a_xb_x-2a_x^2+3b_x^2+3b_y^2}}}=\frac{7a_xb_y}{\sqrt{\left(7a_xb_y\right)^2+\left(5a_xb_x-2a_x^2+3b_x^2+3b_y^2\right)^2}}$$
which, again after a lot of algebraic manipulation, comes to $$\sin{F\hat{H}G}=\frac{7a_xb_y}{\sqrt{4a_x^4-20b_xa_x^3+\left(13b_x^2+37b_y^2\right)a_x^2+30b_x\left(b_x^2+b_y\right)^2a_x+9\left(b_x^2+b_y^2\right)^2}}$$
which is in fact equal to $$\sin{F\hat{H}G}=\frac{7a_xb_y}k$$
Now, we can find the area $A$ of the green triangle $$A=\frac{(HF)(HG)}2\sin{F\hat{H}G}\\
\Rightarrow A=\frac{\frac k{98}\times 7a_xb_y}k\\
\Rightarrow A=\frac{a_xb_y}{14}$$
The area $A'$ of the largest triangle is $\dfrac{a_xb_y}2$
Therefore, the answer to the question is $$\dfrac{A}{A'}=\dfrac{\frac{a_xb_y}{14}}{\frac{a_xb_y}2}=\frac17$$
Teachers' Resources
Why do this problem?
This problem offers students the opportunity to discover and prove a result about triangles divided into smaller areas. We hope there will be a moment of surprise leading to curiosity as students desire to explain the result. Students might tackle the problem using ratios and similar triangles, or they might use it to practise manipulating vectors.
This would be a good problem for students to explore using dynamic geometry software such as GeoGebra.
Possible approach
Students may benefit from working on Triangle in a Triangle and Areas and Ratios before tackling this problem.

Begin by sharing the diagram above and explaining to students how it was created - each line joins a vertex to a point $\frac13$ of the way along the opposite side. Ask students to guess what fraction of the area is shaded green - they may wish to suggest a lower and upper bound rather than guessing an exact amount.
Then invite them to consider ways of finding the exact area.
Below are the series of hints from the problem, which you could offer to students as they are working.
The base of triangle $a+f+e$ is $\tfrac{1}{3}$ of the base of the whole triangle.
Can you use this to work out the area of $a+f+e$ as a fraction of the whole triangle?

What about $a+b+c$ and $c+d+e$?
But none of these tell us anything about $g$.
But we do know that $a$, $b$, $c$, $d$, $e$, $f$ and $g$ together make the whole triangle!
Can we combine all this to find an expression for $g$ in terms of other areas?
It would be useful to know the areas of the little blue triangles...

We know that:
- $a$ has the same height as triangle $ECB$.
- Triangle $ECB$ is $\tfrac{1}{3}$ of the whole triangle
If we can find the length $EH$ as a fraction of $HB$, we could work out the area of the blue triangle...
Sometimes it helps to add in an extra line...

Can you find some similar triangles in this diagram?
How does $EJ$ compare with $AF$?
How does $EJ$ compare with $BF$
How does $EH$ compare with $HB$?
How does $EH$ compare with $EB$?
Alternatively, if you want your students to focus on vector methods, you could share a diagram such as the one below, in which vectors $\bf{x}$ and $\bf{y}$ have been defined such that $\overrightarrow{AC}=3\bf{x}$ and $\overrightarrow{AB}=3\bf{y}$.

Key questions
Can you express $\overrightarrow{DC}$ in terms of $\bf{x}$ and $\bf{y}$?
Can you express $\overrightarrow{BE}$in terms of $\bf{x}$ and $\bf{y}$?
By writing $\overrightarrow{DG}$ as $\lambda \overrightarrow{DC}$ and $\overrightarrow{BG}$ as $\mu \overrightarrow{BE}$, can you find two expressions for $\overrightarrow{AG}$?
By equating coefficients of $\bf{x}$ and $\bf{y}$, can you find $\lambda$?
Possible extension
Students could explore what happens if a fraction other than $\frac13$ is chosen to divide the sides of the original triangle.
Possible support
Triangle in a Triangle is a more accessible problem on a similar theme.
