Getting Round the City
In a city with a grid system of roads, how do you get from A to B?
Problem
This resource is part of "Dotty Grids - Exploring Distance"
Getting Round the City printable sheet
The grid below represents a city laid out in "blocks" with all the roads running north-south, or east-west.
Imagine two friends live where the red and blue dots are on the grid.
Image
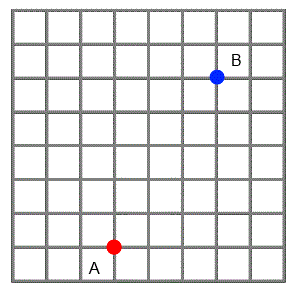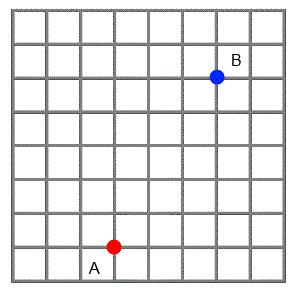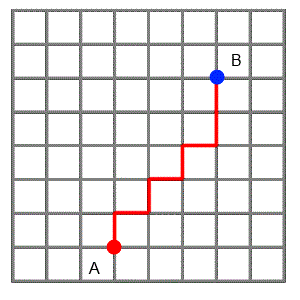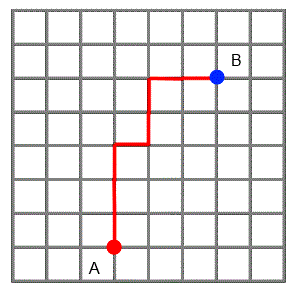
The animation shows three paths that one friend could choose if he wanted to visit the other. He likes to find the shortest routes possible, so he always travels north or east, never south or west.
What interesting mathematical questions could you explore on a city grid like this one?
Click below for some ideas.
How many different paths are there from A to B?
If I know the coordinates of two points, can I quickly work out how far I will have to walk to get from one to the other?
Is there a quick way to find all the different paths from one point to another?
Is there a quick way to work out how many different paths there will be?
If I start at a point and only want to walk 6 blocks, how many possible places might I end up?
Student Solutions
Annette from Copleston Sixth Form explains why there are $56$ possible routes from $A$ to $B$:
All routes between $A$ and $B$ will be equal in length as you need to
travel $3$ east and $5$ north in any order. In total there are $56$ different
paths leading to $B$.
The number in each square represents the number of possible paths from $A$ to that square.
It is worked out like this:
because you must arrive at a square from the point either directly south or directly west of it.
Leah from St. Stephen's School Carramar found a general rule for the number of ways of travelling from point $(x_1,y_1)$ to $(x_2,y_2)$ going only north and east and discussed some ways to find the number of paths from $A$ to $B$:
If the route must be taken without crossing diagonally, it will take $(x_2-x_1) + (y_2-y_1)$
units to reach the opposite point.
E.g the points $(0,1)$ and $(3,6)$, a path will be $(6-0)+(3-1) = 8$ units long.
Number of paths from $(x_1,y_1)$ to $(x_2,y_2)$ = number of paths consisting of $(x_2-x_1)$ steps east and $(y_2-y_1)$ steps north, in some order
$ =$ ${(x_2-x_1)+(y_2-y_1)}\choose{(x_2-x_1)}$ $= \frac{[(x_2-x_1)+(y_2-y_1)]!}{(x_2-x_1)!(y_2-y_1)!}$
How many paths are there from $A$ to $B$?
$\frac{(5+3)!}{5!3!} = 56$.
Alternative methods :
- Drawing a tree diagram via labeling each node as a
letter, which gives $56$ options.
-Drawing out all the possible routes.
Hannah from Burntwood explains how many different paths we can take if we only want to travel $6$ blocks:
A good way to think about this is as a tree diagram.
At the starting point, you have $4$ options of where to go.
Then at each subsequent point you have a choice of $3$ paths (assuming you can't double back on yourself)
So, the formula would be $4 \times 3^{(n-1)}$, where $n$=the number of blocks you walk.
In this case, $n=6$, so there are $4x3^5= 972$ paths.
Thank you to everyone who submitted a solution to this problem!
All routes between $A$ and $B$ will be equal in length as you need to
travel $3$ east and $5$ north in any order. In total there are $56$ different
paths leading to $B$.
| $1$ | $6$ | $21$ | $56$ ($B$) |
| $1$ | $5$ | $15$ | $35$ |
| $1$ | $4$ | $10$ | $20$ |
| $1$ | $3$ | $6$ | $10$ |
| $1$ | $2$ | $3$ | $4$ |
| $A$ | $1$ | $1$ | $1$ |
The number in each square represents the number of possible paths from $A$ to that square.
It is worked out like this:
| $M$ | $M+N$ |
| - | $N$ |
because you must arrive at a square from the point either directly south or directly west of it.
Leah from St. Stephen's School Carramar found a general rule for the number of ways of travelling from point $(x_1,y_1)$ to $(x_2,y_2)$ going only north and east and discussed some ways to find the number of paths from $A$ to $B$:
If the route must be taken without crossing diagonally, it will take $(x_2-x_1) + (y_2-y_1)$
units to reach the opposite point.
E.g the points $(0,1)$ and $(3,6)$, a path will be $(6-0)+(3-1) = 8$ units long.
Number of paths from $(x_1,y_1)$ to $(x_2,y_2)$ = number of paths consisting of $(x_2-x_1)$ steps east and $(y_2-y_1)$ steps north, in some order
$ =$ ${(x_2-x_1)+(y_2-y_1)}\choose{(x_2-x_1)}$ $= \frac{[(x_2-x_1)+(y_2-y_1)]!}{(x_2-x_1)!(y_2-y_1)!}$
How many paths are there from $A$ to $B$?
$\frac{(5+3)!}{5!3!} = 56$.
Alternative methods :
- Drawing a tree diagram via labeling each node as a
letter, which gives $56$ options.
-Drawing out all the possible routes.
Hannah from Burntwood explains how many different paths we can take if we only want to travel $6$ blocks:
A good way to think about this is as a tree diagram.
At the starting point, you have $4$ options of where to go.
Then at each subsequent point you have a choice of $3$ paths (assuming you can't double back on yourself)
So, the formula would be $4 \times 3^{(n-1)}$, where $n$=the number of blocks you walk.
In this case, $n=6$, so there are $4x3^5= 972$ paths.
Thank you to everyone who submitted a solution to this problem!
Teachers' Resources
For ideas on how this problem and others from the Dotty Grids Collections can be used in the classroom, you may be interested to read this article.
A printable version of this problem is available as a Word or Pdf file.
