problem
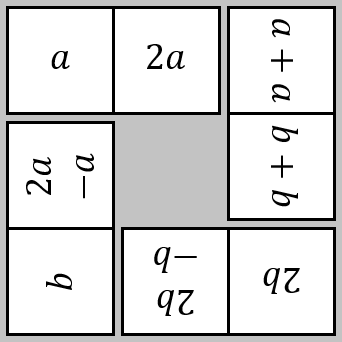
Warmsnug double glazing
Age
14 to 16
Challenge level
How have "Warmsnug" arrived at the prices shown on their windows? Which window has been given an incorrect price?
problem
Which is cheaper?
Age
14 to 16
Challenge level
When I park my car in Mathstown, there are two car parks to choose from. Can you help me to decide which one to use?
problem
Nutrition and cycling
Age
14 to 16
Challenge level
Andy wants to cycle from Land's End to John o'Groats. Will he be able to eat enough to keep him going?
problem
Isosceles seven
Age
14 to 16
Challenge level
Is it possible to find the angles in this rather special isosceles triangle?
problem
Of all the areas
Age
14 to 16
Challenge level
Can you find a general rule for finding the areas of equilateral triangles drawn on an isometric grid?
problem
Fair shares?
Age
14 to 16
Challenge level
A mother wants to share a sum of money by giving each of her
children in turn a lump sum plus a fraction of the remainder. How
can she do this in order to share the money out equally?
problem
What's possible?
Age
14 to 16
Challenge level
Many numbers can be expressed as the difference of two perfect squares. What do you notice about the numbers you CANNOT make?
problem
Pick's theorem
Age
14 to 16
Challenge level
Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Find a relationship between p, i and the area of the polygons.
problem
Painted cube
Age
14 to 16
Challenge level
Imagine a large cube made from small red cubes being dropped into a pot of yellow paint. How many of the small cubes will have yellow paint on their faces?
problem
Triangle in a triangle
Age
14 to 16
Challenge level
Can you work out the fraction of the original triangle that is covered by the inner triangle?
problem
Nicely similar
Age
14 to 16
Challenge level
If the hypotenuse (base) length is 100cm and if an extra line splits the base into 36cm and 64cm parts, what were the side lengths for the original right-angled triangle?
problem
Surprising transformations
Age
14 to 16
Challenge level
I took the graph y=4x+7 and performed four transformations. Can you find the order in which I could have carried out the transformations?
problem
Latin numbers
Age
14 to 16
Challenge level
Can you create a Latin Square from multiples of a six digit number?