What's possible?
Many numbers can be expressed as the difference of two perfect squares. What do you notice about the numbers you CANNOT make?
Problem
What's Possible? printable worksheet
You may be interested in Hollow Squares which offers an alternative way of thinking about the same underlying mathematics.
Many numbers can be expressed as the difference of two perfect squares. For example,
$$20 = 6^2 - 4^2$$
$$21 = 5^2 - 2^2$$
$$36 = 6^2-0^2$$
How many of the numbers from $1$ to $30$ can you express as the difference of two perfect squares?
Here are some questions to consider:
What do you notice about the difference between squares of consecutive numbers?
What about the difference between the squares of numbers which differ by $2$? By $3$? By $4$...?
When is the difference between two square numbers odd?
And when is it even?
What do you notice about the numbers you CANNOT express as the difference of two perfect squares?
You may want to take a look at Plus Minus next.
Getting Started
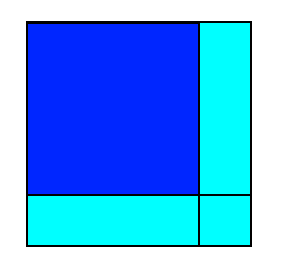
You may find this image helpful when proving your findings.
Student Solutions
Hannah from Munich International School worked out which numbers between 1 and 30 were possible:
1: $1^2 - 0^2$ is $1 - 0 = 1$
2: does not work
3: $2^2 - 1^2$ is $4 - 1 = 3$
4: $2^2 - 0^2$ is $4 - 0 = 4$
5: $3^2 - 2^2$ is $9 - 4 = 5$
6: does not work
7: $4^2 - 3^2$ is $16 - 9 = 7$
8: $3^2 - 1^2$ is $9 - 1 = 8$
9: $5^2 - 4^2$ is $25 - 16 = 9$
10: does not work
11: $6^2 - 5^2$ is $36 - 25 = 11$
12: $4^2 - 2^2$ is $16 - 4 = 12$
13: $7^2 - 6^2$ is $49 - 36 = 13$
14: does not work
15: $8^2 - 7^2$ is $64 - 49 = 15$
16: $5^2 - 3^2$ is $25 - 9 = 16$
17: $9^2 - 8^2$ is $81 - 64 = 17$
18: does not work
19: $10^2 - 9^2$ is $100 - 81 = 19$
20: $6^2 - 4^2$ is $36 - 16 = 20$
21: $11^2 - 10^2$ is $121-100 = 21$
22: does not work
23: $12^2 - 11^2$ is $144-121=23$
24: $7^2-5^2$ is $49 - 25 = 24$
25: $13^2 - 12^2$ is $169-144=25$
26: does not work
27: $14^2 - 13^2$ is $196 - 169 = 27$
28: $8^2 - 6^2$ is $64-36 = 28$
29: $15^2 - 14^2$ is $225 - 196 = 29$
30: does not work
You can express 22 of the 30 numbers as a difference of two perfect squares. A pattern occuring throughout these solutions is that all odd numbers can be represented by a difference of two perfect squares, as well as all numbers resulting in an integer when divided by four.
Joshua from St John's School used algebra to show how odd numbers and multiples of four could be made:
You can make every odd number by taking consecutive squares.
$(n+1)^2 - n^2 = 2n+1$, every odd number can be written in the form $2n+1$.
Similarly, you can make every multiple of 4 by taking squares with a difference of 2.
All other numbers you can't make:
$(n+x)^2 - n^2 = x^2 + 2nx = x(x+2n)$
If $x$ is odd then $x^2$ is also odd and $2nx$ is even. An odd plus an even is odd.
If $x$ is even then $x^2$ is a multiple of $4$ and $2nx$ is also a multiple of $4$ so $(n+x)^2 - n^2$ is a multiple of $4$.
Numbers such as 2,6,10 etc can't be made because these are made by multiplying an even by an odd.
Patrick from Woodbridge School and Richard from Mearns Castle School both used a formula for the difference of two squares to investigate which numbers were possible. Here is Patrick's solution:
$a^2 - b^2= (a + b)(a - b)$
Thus, a number $n$ can only be a difference of two squares if it has two factors of the form $(a + b)$ and $(a - b)$, where $a + b \geq \sqrt{n}$ and $a - b \leq \sqrt{n}$.
If $1$ could be written as the difference of squares then $(a + b) = (a - b) = 1$, as the only factor of $1$ is $1$.
Thus, $a = 1$ and $b = 0$. So $1 = 1^2 - 0^2$.
If $2$ could be written as the difference of two squares then $(a + b) = 2$ and $(a - b) = 1$, as $2$ is prime, and clearly $a - b < a + b$ for positive $b$.
Thus, solving the simultaneous equations, $b = 2 - a$, so $a - (2 - a) = 1$, $2a = 3$ and $a = \frac{3}{2}$. Thus, $2$ is not representable as the difference of two integer squares.
This method can be generalised for any prime $p$ by solving $(a + b) = p$ and $(a - b) = 1$
Adding the equations gives $2a = p + 1$, so $a = \frac{p+1}{2}$. Since $a - b = 1$, $b = a-1$, so $b = \frac{p+1}{2} - 1 = \frac{p-1}{2}$. Thus, any odd prime can be written as the difference of two squares.
Any square number $n$ can also be written as the difference of two squares, by taking $a = \sqrt{n}$ and $b = 0$.
Generally, a number can be written as the difference of two squares if it has two factors of the same parity, since if $a + b$ is odd and $a - b$ is even, when the two equations are added we would get $2a$ odd, so the solution would not be an integer. So a number cannot be written as a difference of two squares if and only if it is equivalent to $2$ mod $4$ (leaves a remainder of $2$ when divided by $4$).
Richard from Comberton Village College considered prime factorisation:
An integer $x$ can be written as the difference between two square integers unless it contains only one $2$ in its prime power factorisation.
Proof: $x=a^2 - b^2$ can be rewritten in the form $(a+b)(a-b)$.
Suppose $u$ and $v$ are two factors of $x$ such that $u = a + b$ and $v = a - b$.
Subtracting the two equations, we get $u - v = 2b$.
This tells us that the difference between the two factors will always be even if the number can be written in this form.
Now, to get an even difference, we either need $u$ and $v$ to be both odd, or both even. Therefore, any number with either two even or odd factors can be written in this form.
This leaves numbers which will always have one odd and one even factor.
If $v$ is an odd factor of $x$, it must have a prime factorisation of only odd numbers.
Suppose $u$ is an even factor of $x$ and contains more than one $2$ in its prime factorisation.
This means that $u$ could be divided by two and still be even, and at the same time $v$ could be doubled so that it too is even. This means that $x$ has a factor pair which are both even, and so can be written as the difference of two squares.
If both factors are odd an even difference will also be attained, so if there are no twos in the prime factorisation of $x$, then x can be written as the difference of two squares.
This leaves the case where there is exactly one $2$ in the prime factorisation. This means that one factor must contain the $2$ and not the other, and that the factors cannot be manipulated in the fashion described before. This will always leave factors with an odd difference suggesting $x$ cannot be written as the difference of two squares.
This also gives a very nice algorithm for finding two squares which have a difference of $x$:
1. Establish how many $2$s are in the prime factorisation of $x$. If there is only one, x cannot be written as the difference of two squares.
2. Choose a factor pair which are both even or both odd, call them $u$ and $v$. Find their difference and divide it by 2 to find the smaller square. $\frac{u - v}{2}=b$ from before.
3. Square $b$ and add it to $x$. Square root the sum and that is $a$.
We now have $x = a^2 - b^2$.
For example, $60 = 2 \times 2 \times 3 \times 5$. There is more than one 2 so it is possible.
The two factors $2 \times 5 = 10$ and $2 \times 3 = 6$ give a difference of 4. Halve it to get $b = 2$.
$x + b^2 = 60 + 4 = 64$. $\sqrt{64} = 8$, so $a = 8$.
This gives us $60 = 8^2 - 2^2$.
We could also have taken $u = 2 \times 3 \times 5$ and $v = 2$, which gives a difference of 28. Halve it to get $b=14$.
$x + b^2 = 60 + 196 = 256$.
$\sqrt{256} = 16$ so $a = 16$.
$16^2 - 14^2 = 60$
Teachers' Resources
Why do this problem?
This problem starts by asking students to find which numbers can be expressed as the difference of two square numbers, and then suggests some possible avenues for exploration. This can then be used as a springboard to generalisations and the use of algebra for justifications and proof. Along the way, students have the opportunity to make use of the important identity $a^2 - b^2 = (a + b)(a - b)$.
An alternative to this problem which some students may find more accessible is Hollow Squares.
Possible approach
This printable resource may be useful: What's Possible? worksheet.
You may wish to introduce the problem like this:
Ask students for a two-digit number under 30. Write it on the board and express it as the difference between two squares. Repeat several times.
Challenge students to find all numbers between 1 and 30 that can be expressed as the difference of two squares. Encourage them to find more than one solution where possible.
Once students have had time to find most of the answers, ask them to share what they found and list their answers on the board.
'Have a look at the results so far. What do you notice?'
Give students a couple of minutes to talk to their partners before bringing the class back together.
Here are some of the conjectures and questions that may emerge:
- The difference between squares of consecutive numbers is always odd.
- The difference between squares of consecutive numbers is equal to the sum of the consecutive numbers.
- What happens to the difference when I square two numbers that differ by 2?
- Numbers that can be made in more than one way have lots of factors.
- When is the difference between two square numbers odd?
- And when is it even?
- Why are some numbers impossible to make?
- Can we predict which numbers are impossible to make?
Alternatively, you could introduce the problem like this:
Bring the class back together and invite those students who have useful insights to share them with the class. You may wish to introduce an algebraic and a geometric approach to proving one particular conjecture: for example, that the difference between consecutive squares is always odd. A diagrammatic method for calculating the difference of two squares is explored in the problem Plus Minus.
Now give the class some time to work on proving their conjectures.
You may also wish to set the following challenge:
"In a while, I'm going to give you a number and ask you to quickly find one or more ways to write it as the difference of two squares, or to convince me that it can't be done. Can you develop a strategy that will help you do this?"
Your plenary could involve students presenting their findings to the rest of the class. Expect students to be clear and rigorous in their justifications. Encourage them to challenge any proofs that lack clarity and rigour, and suggest ways of improving them.
Key questions
Possible extension
Possible support
| 1 | 2 | 3 | |
| 1 | $1^2-0^2$ | ||
| 2 | |||
| 3 | $2^2-1^2$ | ||
| 4 | $2^2-0^2$ | ||
| 5 | $3^2-2^2$ | ||
| 6 | |||
| 7 | $4^2-3^2$ | ||
| 8 | $3^2-1^2$ | ||
| 9 | $5^2-4^2$ | $3^2-0^2$ |
