You may also like

Compare Areas

Which has the greatest area, a circle or a square, inscribed in an isosceles right angle triangle?

Take a Square

Cut off three right angled isosceles triangles to produce a pentagon. With two lines, cut the pentagon into three parts which can be rearranged into another square.

Semi-detached

A square of area 40 square cms is inscribed in a semicircle. Find the area of the square that could be inscribed in a circle of the same radius.

Warmsnug Double Glazing

Age 14 to 16
Challenge Level

Warmsnug Double Glazing printable worksheet


Warmsnug calculate the prices of their windows according to the area of glass used and the length of frame needed.

Can you work out how Warmsnug arrived at the prices of the windows below?
Which window has been given an incorrect price?

windows

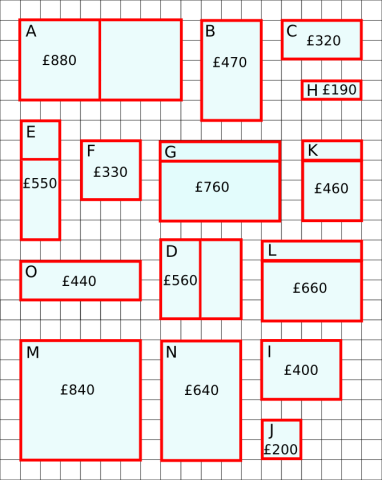
This spreadsheet generates prices for the windows according to different pricing rules.
Can you find an efficient strategy for finding how the prices were calculated?

 

 

 

This problem is based on the original Warmsnug Double Glazing problem which appeared in The Language of Functions and Graphs produced by the Shell Centre for Mathematical Education and the Joint Matriculation Board.

 

 

 

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.
Copyright © 1997 - 2023. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.