Reasoning, convincing and proving

problem
Natural sum

Age

14 to 16

Challenge level

The picture illustrates the sum 1 + 2 + 3 + 4 = (4 x 5)/2. Prove the general formula for the sum of the first n natural numbers and the formula for the sum of the cubes of the first n natural numbers.
problem
Exhaustion

Age

16 to 18

Challenge level

Find the positive integer solutions of the equation (1+1/a)(1+1/b)(1+1/c) = 2
problem
Proximity

Age

14 to 16

Challenge level

We are given a regular icosahedron having three red vertices. Show that it has a vertex that has at least two red neighbours.
problem
Picture story

Age

14 to 16

Challenge level

Can you see how this picture illustrates the formula for the sum of the first six cube numbers?
problem
Summats clear

Age

16 to 18

Challenge level

Find the sum, f(n), of the first n terms of the sequence: 0, 1, 1, 2, 2, 3, 3........p, p, p +1, p + 1,..... Prove that f(a + b) - f(a - b) = ab.
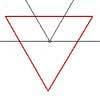
problem
Napoleon's hat

Age

16 to 18

Challenge level

Three equilateral triangles ABC, AYX and XZB are drawn with the point X a moveable point on AB. The points P, Q and R are the centres of the three triangles. What can you say about triangle PQR?
problem
Shape and territory

Age

16 to 18

Challenge level

If for any triangle ABC tan(A - B) + tan(B - C) + tan(C - A) = 0 what can you say about the triangle?
problem
Areas and ratios

Age

16 to 18

Challenge level

Do you have enough information to work out the area of the shaded quadrilateral?
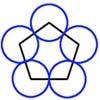
problem
Polycircles

Age

14 to 16

Challenge level

Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
problem
OK! Now prove it

Age

16 to 18

Challenge level

Make a conjecture about the sum of the squares of the odd positive integers. Can you prove it?