Arithmetic sequences
-

-
 problemFavourite
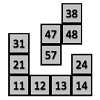
problemFavouriteBuzzy Bee
Buzzy Bee was building a honeycomb. She decorated the honeycomb with a pattern using numbers. Can you discover Buzzy's pattern and fill in the empty cells for her?
-

-
-
 problemFavourite
problemFavouriteMissing Middles
Can you work out the domino pieces which would go in the middle in each case to complete the pattern of these eight sets of three dominoes?
-
 problemFavourite
problemFavouriteDoplication
We can arrange dots in a similar way to the 5 on a dice and they usually sit quite well into a rectangular shape. How many altogether in this 3 by 5? What happens for other sizes?
-
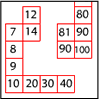 problemFavourite
problemFavouriteMultiplication Square Jigsaw
Can you complete this jigsaw of the multiplication square?
-

-
 problemFavourite
problemFavouriteDays and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...
-
 problemFavourite
problemFavouritePicturing Square Numbers
Square numbers can be represented as the sum of consecutive odd numbers. What is the sum of 1 + 3 + ..... + 149 + 151 + 153?
