Subtended Angles
What is the relationship between the angle at the centre and the angles at the circumference, for angles which stand on the same arc? Can you prove it?
Problem
This problem has now been superseded by Circumference Angles
In this problem you can make use of the interactivity below.
Choose two points on the edge of the circle. Call them $A$ and $B$.
Join these points to the centre, $C$. What is the angle at $C$?
Join $A$ and $B$ to a point on the edge. Call that point $D$. What is the angle at $D$?
What do you notice?
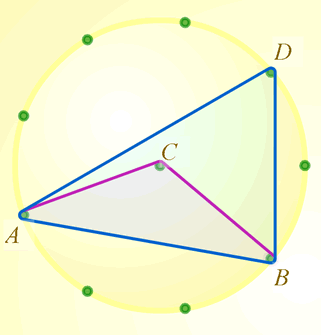
Would the same thing happen if $D$ took a different position on the edge of the circle?
Would the same thing happen if you started with a different two points on the edge of the circle?
Would the same thing happen if you started with any two points on the edge of any circle?
Can you prove it?
For printable sets of circle templates for use with this activity, please see Printable Resources page.
Many thanks to Geoff Faux who introduced us to the merits of the 9 pin circular geo-board.
The boards, moulded in crystal clear ABS that can be used on an OHP (185 cm in diameter), together with a teacher's guide, are available from Geoff at Education Initiatives
Getting Started
If you are having difficulty with the interactivity, you may find this helpful:
Join all the points up to the centre and look for isosceles triangles.
You may find this diagram helpful to get you started.
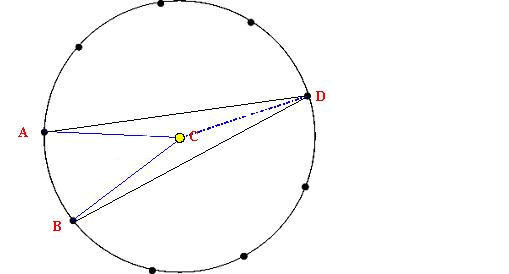
It is useful to note that the blue lines are all radii of the circle, and as such, are all the same length. You may want to use some algebra to help explain your proof .
Student Solutions
Arun from the National Public School in Bangalore sent us this detailed solution:
It is clearly seen that the angle at $C$ is twice the angle at $D$. Here we have the fundamental theorem with regard to angles in circles -
" the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the circle "
This can be proved as follows :
Given a circle $(C,r)$ in which arc $AB$ subtends angle ($ACB$) at the centre and angle ($ADB$) at any point $D$ on the circle.
To Prove:
(i) angle $(ACB)$ = $2\times$angle $(ADB)$, when arc $AB$ is a minor arc or a semicircle.
(ii) Reflex angle $(ACB) = 2\times$ angle $(ADB)$, when arc $AB$ is a major arc
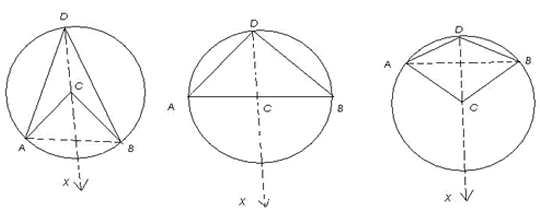
Construction: Join $AB$ and $DC$. Produce $DC$ to a point $X$ outside the circle.
Clearly, there are 3 cases.
Case I : arc $AB$ is a minor arc [Fig (i)]
Case II : arc $AB$ is a semicircle [Fig (ii)]
Case III : arc $AB$ is a major arc [Fig (iii)]
We know that when one side of a triangle is produced then the exterior angle so formed is equal to the sum of the interior opposite angles.
Therefore,
angle $(ACX)$ = angle $(CAD)$ + angle $(CDA)$ [consider triangle $CAD$]
angle $(BCX)$ = angle $(CBD)$ + angle $(CDB)$ [consider triangle $CBD$]
But,
angle $(CAD)$ = angle $(CDA)$ [since $CD = CA = r$ ] and ,
angle $(CBD)$ = angle $(CDB)$ [since $CD = CB = r$ ]
Therefore,
angle $(ACX) = 2\times$ angle $(CDA)$ and
angle $(BCX) = 2\times$angle $(CDB)$
In Fig (i) and Fig (ii) ,
angle $(ACX)$ + angle $(BCX)$ = $2 \times$ angle $(CDA)$ + $2\times$ angle $(CDB) \Rightarrow$
angle $(ACB)$ = $2$[angle $(CDA)$ + angle $(CDB)$] $\Rightarrow$
angle $(ACB)$ = $2 \times$angle $(ADB)$
in Fig (iii),
angle $(ACX)$ + angle $(BCX)$ = $2\times$ angle $(CDA)$ + $2\times$ angle $(CDB) \Rightarrow$
reflex angle $(ACB)$ = $2$[angle $(CDA)$ + angle $(CDB)$] $\Rightarrow$
reflex angle $(ACB)$ = $2\times $ angle $(ADB)$
Hence proved.
This theorem has 2 main implications:
(i) The angle in a semicircle is a right angle .
i.e. in fig (2), where arc $AB$ is a semicircle, or in other words $ACB$ is a diameter,
angle $(ADB) = \frac{1}{2} \times$ angle $(ACB) = \frac{1}{2}\times$($180$ degrees) = $90$ degrees = a right angle
This holds true for any position of point $C$ on the semicircle.
(ii) Angles in the same segment of a circle are equal.
This means that if an arc subtends $2$ angles, at $2$ different points on the circle, these angles will be equal.
We can prove this, by proving that each of the $2$ angles is equal to half the angle subtended at the centre.
Teachers' Resources
Why do this problem?
Teachers may find the article Angle Measurement: an Opportunity for Equity of interest.
Possible approach
Demonstrate how the geoboard works - clicking on a coloured rubber band, dragging it onto a peg and then "stretching" it out onto two more pegs to make a triangle.
Draw a triangle that encloses the centre, split it into three isosceles triangles and find the angles.
An example may look like this:
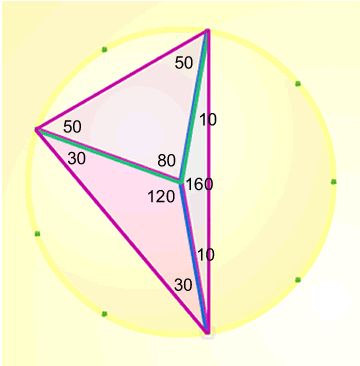
"The angles around the centre add up to 360 degrees and the angles at the vertices add up to 180 degrees. What else do you notice about angles at the centre and angles at the vertices?"
Ask students to take a look at their working for Triangles in Circles to identify general rules that work in all cases. Encourage students to consider all the different possible angles at the circumference subtending a specific arc.
When the angle at the centre is a reflex angle, students may need some help to see that the angle at the circumference is still half the angle at the centre. For example:
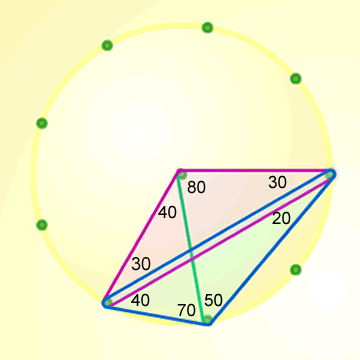
A Virtual Geoboard allows you to create triangles in circles with a variable number of pegs. Ask students to check that the relationship between angles at the centre and angles at the circumference holds in 10 peg, 12 peg, 15 peg ... circles.
Key questions
- What is the relationship between the angle at the centre and the angle at the circumference?
- What do we know already that might be useful here?
- What are the implications of our findings? (How can other circle theorems be deduced from this one?)
Possible extension
- Would the same thing happen if you started with an arc between any two points on the circumference of any circle?
- Can you prove it?
Possible support

