Steel Cables
Some students have been working out the number of strands needed for different sizes of cable. Can you make sense of their solutions?
Problem
Steel Cables printable worksheet
Cables can be made stronger by compacting them together in a hexagonal formation.
Here is a 'size 5' cable made up of 61 strands:

How many strands are needed for a size 10 cable?
How many for a size n cable?
Can you justify your answer?
Once you've had a go at the problem, click below to see the diagrams some students produced when they worked on it.
Do these diagrams give you any ideas for how you could work out the number of strands needed?
Group 1
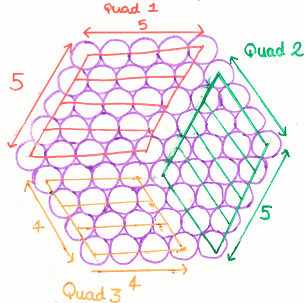
Group 2

Group 3
Group 4
The work that these students did using their diagrams is given on the Getting Started page, if you would like another hint.
Which of the four approaches makes the most sense to you?
What do you like about your favourite approach?
Can you think of any other approaches?
Notes and Background
Hexagonal packings are often chosen for strength or efficiency. To read more about packings, take a look at the Plus articles Mathematical Mysteries: Kepler's Conjecture and Newton and the Kissing Problem
Getting Started
Do you know a quick way of adding up all the numbers from 1 to n?
If not, take a look at the problem Picturing Triangle Numbers.
Below are student diagrams from the problem page, but they now also show the working that the students used to explain their diagrams. Can you explain their reasoning?
Group 1


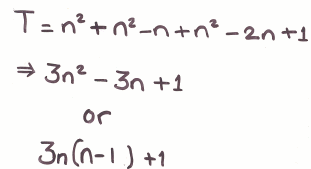
Group 2


Group 3


Group 4


If you are finding it difficult to make sense of the different groups' work, try to work out what they might have drawn for a size 6 cable.
Student Solutions
Rohan from Stephen Perse Foundation in the UK used this geometrical method:
I started by taking 'size 2' and 'size 3' hexagons.
If you split the spapes into two like below, you can easily find the $n$th term for each.


If you take the part on the right, you can see it is a square number. It seems to be the square of the number one less than the 'size', therefore $(n-1)^2$.
For the part on the left, there are a certain number of rows, with 'side' on each row. Therefore, it is a multiple of $n.$ For 'size' $2,$ it is $3\times n.$ For 'size' $3,$ it is $5\times n.$ $3$ is $2\times2-1$ and $5$ is $3\times2-1.$ Therefore it is $2n-1$ multiplied by $n,$ or $n(2n-1)$ or $2n^2-n.$
Combining the two together you get $2n^2-n+(n-1)^2.$
Sanika from India used a similar but different method:
I divided the hexagon into 2 trapeziums like the picture shows:
I then assumed that 1 circle represented 1 unit and calculated the area of both the trapeziums using the formula $2\times\left(h\frac{N + b}2\right).$ I then proceeded to subtract [$b$ from the result] as it was added twice. So the final equation was $h(N + b)-b.$ So $N$ would be the size of the cable, $b$ would be $2N-1$ and $h$ would again be the size of the cable as it represents the height.
So in a size $10$ cable, $N$ would be $10,$ $b$ would be $19$ and $h$ would be $10.$ Inserting these values into our formula, we get $10(29)-19= 271.$
Brady from Canada sent us a similar solution:

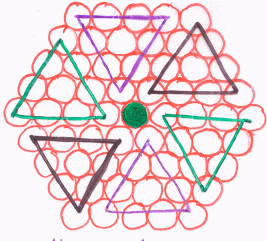
We can break a size $n$ hexagon into $3$ big triangles (of side length $n$) and 3 small triangles (of side length $n-2$). Since the $3$ big triangles meet in the middle, when we add up the number of strands in each we have to subtract $2$ because we have overcounted the middle strand by $2$:
$\frac{3n(n+1)}{2}$ + $\frac{3(n-2)(n-1)}{2}- 2 = 3n^2 - 3n + 1$
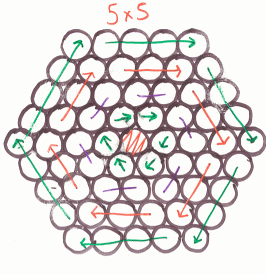
Calvin from Ethiopia and Patrick from Otterbourne used an algebraic approach:
At first I noticed a pattern: the number of strands per cable was going up by multiples of 6 every time. Then I plotted the data for sizes 1-10:
| Size | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Strands | 1 | 7 | 19 | 37 | 61 | 91 | 127 | 169 | 217 | 271 |
and graphed them. The result was a parabola, so I found its equation and that was the answer. The answer is s = 3n2 - 3n + 1, where s is the number of strands required and n is the size of the cable.
Patrick described a method for finding Calvin's formula:
The sequence starts off: 1, 7, 19, 37, 61, ...
If we take the difference between successive terms, we get the sequence 6, 12, 18, 24, ...
If we take successive differences again, we get 6, 6, 6, ...
This is constant, so we must have a quadratic equation s = an$^2$ + bn + c.
In fact, half of 6 is 3, so we know that a = 3. Therefore
s = 3n$^2$ + bn + c
In order to find b and c, we can substitute values in:
(n = 1, s = 1) 1 = 3 + b + c
(n = 2, s = 7) 7 = 12 + 2b + c
and we can solve these simultaneous equations to get b = -3 and c = 1.
Sanika also used an algebraic aproach to check the result from the trapezium method:
To verify, I developed a slightly similar method, but this was without using the formula for the area of a trapezium. I again divided the hexagon into $2$ trapeziums and noticed that there would be $N$ rows in each trapezium wherein, consecutive rows will have one more strand than the previous one. Therefore, the total number of strands would be $(N, N+1, N+2, N+3 .......N + (N-1)).$ Then I proceeded to simplify this using the formula used to find the sum of consecutive numbers.
Sum of consecutive numbers = $\frac x 2 (\text{first number + last number})$
So the value of $x$ here would be the value on $N$ as it stands for the number of terms we are summing up. Substituting $N$ into this formula will give us $\frac{N}{2}(3N-1).$
Since we have $2$ trapeziums, we will multiply this by $2$ and subtract the $(2N-1)$ from the result as it is common between the two trapeziums.
This gives us a final formula of $N(3N-1) - (2N-1).$ Substituting for $N,$ I got $10(29)-19=271$ which was the same result I got earlier.
Therefore the number of strands needed can be given by the formula $N(3N-1) - (2N-1),$ where $N$ is the size of the cable.
Well spotted! This formula was discovered by a mathematician called Gauss, who probably used something like Sanika's trapeziums to figure it out.
Teachers' Resources
Why do this problem?
Many students are accustomed to using number patterns in order to generalise. This problem offers an alternative approach, challenging students to consider multiple ways of looking at the structure of the problem and making sense of other people's approaches, an important part of working mathematically.
The powerful insights from these multiple approaches can help us to derive general formulae, and can lead to students' appreciation of the equivalence of different algebraic expressions.
Possible approach
These printable resources may be useful:
Steel Cables
Steel Cables Intro
Steel Cables Templates
Steel Cables - Methods
Start by showing this image:

"Cables can be made stronger by compacting them together in a hexagonal formation. Here is a 'size 5' cable. Can you work out, without counting every strand, how many strands it contains?"
Give students a short time to consider this and then discuss their ideas in pairs, before bringing the class back together to share their different methods.
Hand out this worksheet, together with these templates, and ask:
"How many strands are needed for a size 10 cable?"
"While you are working on this, keep in mind how your method could be adapted to work out the number of strands needed for any size of cable."
While students are working, circulate and observe any interesting methods that students are using. When the class is ready, bring them back together and invite those students with an interesting method to explain what they did.
"Here is some work done by a group of students in another school, who were asked to find a formula to work out the strands needed for a size n cable."
Arrange the class in groups of four, and hand out one of the four pictures from this worksheet to each student.
"I'd like each of you to make sense of the picture I have given you, and work out how to use it to solve the problem. Then, when you are ready, explain your method to the rest of your group. Finally, your group needs to agree on which of the four approaches makes the most sense to you, and be prepared to justify your choice to the rest of the class."
To finish off, each group can explain to the rest of the class which approach they chose, and why.
Key questions
Is there a quick way of adding up all the numbers from 1 to n?
Look at the picture for a size 5 cable. What might the group have drawn for a size 6 cable?
Possible support
Seven Squares gives lots of simple contexts where formulae emerge by looking at structure rather than number sequences.
Picturing Triangle Numbers, Mystic Rose, and Handshakes introduce students to summing consecutive numbers, which is a feature of several of the solutions used by the groups in the problem.
Possible extension
Challenge students to come up with alternative, elegant ways of computing the number of strands in a size n cable.
The problems Summing Squares and Picture Story lead to formulae for some intriguing sequences through analysis of structure.
To read one teacher's account of using this problem, click here.
