Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Semi-regular Tessellations
Age 11 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Goeun from Bangok Patana School in Thailand sent in this solution, which includes 8 semi-regular tesselations. Can Goeun be sure to have found them all?
Firstly, there are only three regular tessellations which are triangles, squares, and hexagons. To make a regular tessellation, the internal angle of the polygon has to be a diviser of 360. This is because the angles have to be added up to 360 so it does not leave any gaps. For example, we can make a regular tessellation with triangles because 60 x 6 = 360.
Students from Cowbridge Comprehensive School in Wales used this spreadsheet to convince themselves that only 3 polygons can make regular tesselations.
Goeun continued:
We can prove that a triangle will fit in the pattern {3, 4, 3, 3, 4} [given in the problem] because 360 - (90 + 60 + 90 + 60) = 60 which is the internal angle for an equilateral triangle.
There are 8 semi-regular tessellations in total. We know each is correct because again, the internal angle of these shapes add up to 360.
For example, for triangles and squares, 60 $\times$ 3 + 90 $\times$ 2 = 360.
- Triangles & Squares
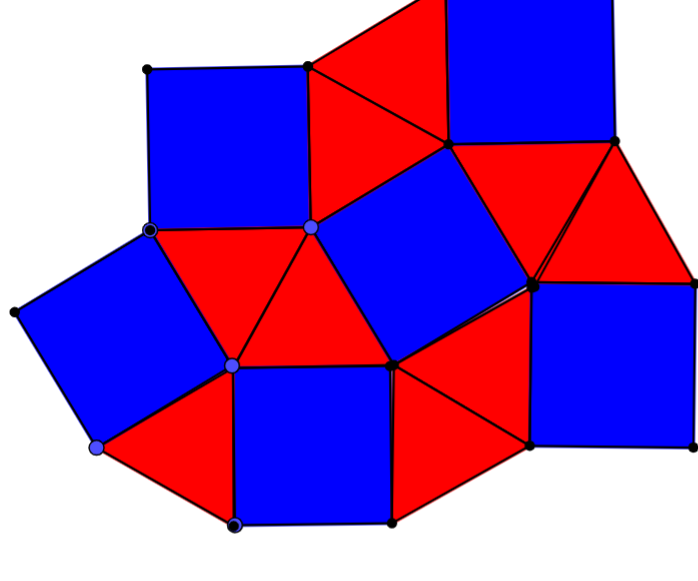
- Triangles & Squares (but a different pattern)
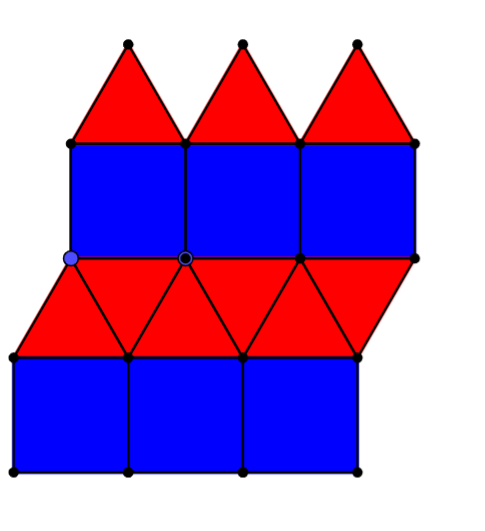
- Hexagons & Triangles
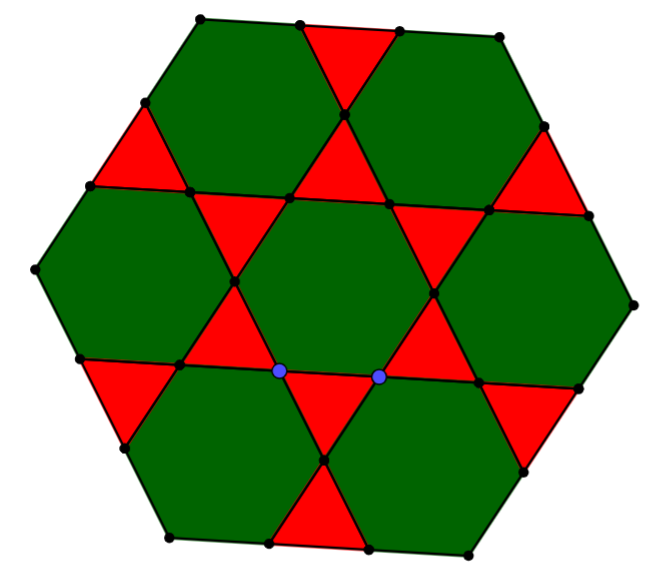
- Hexagons & Triangles (but a different pattern)
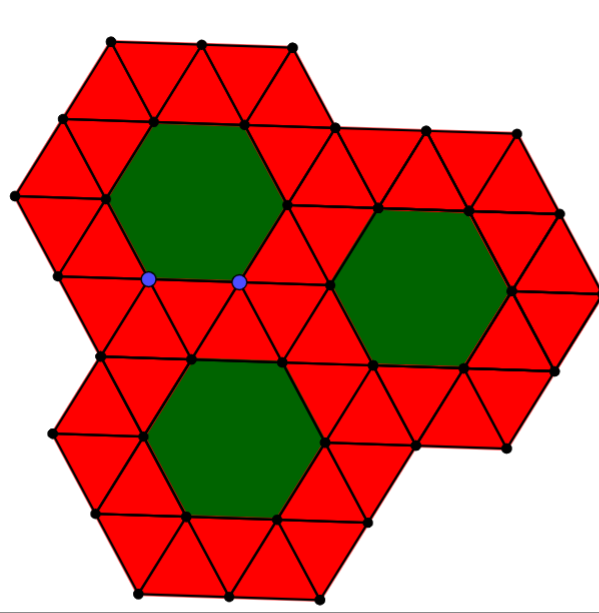
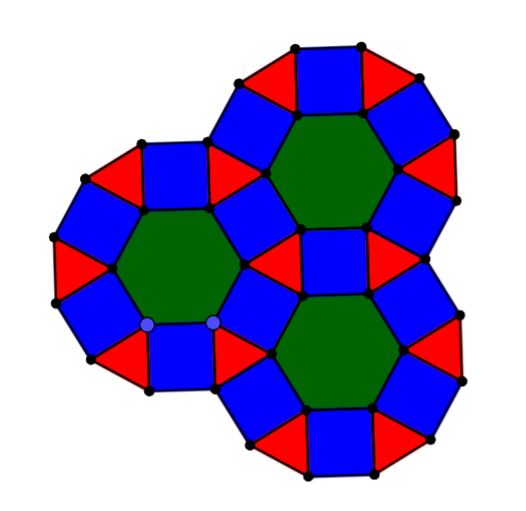
- Hexagons & Triangles & Squares
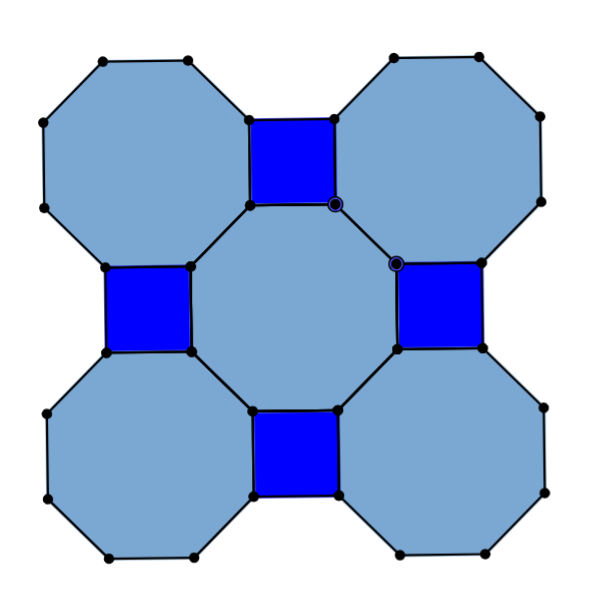
- Octagons & Squares
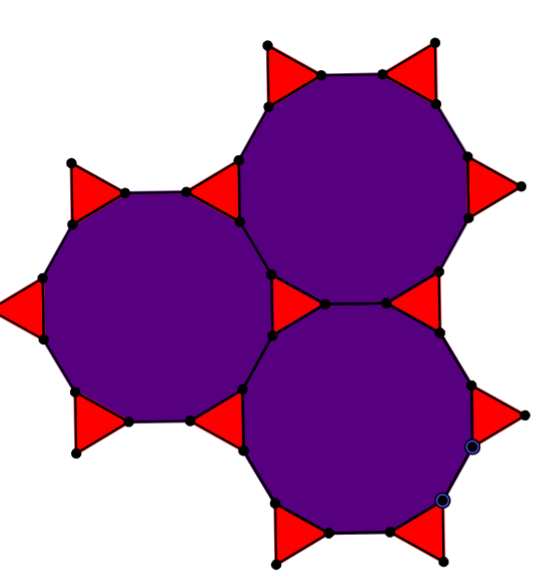
- Dodecagons & Triangles
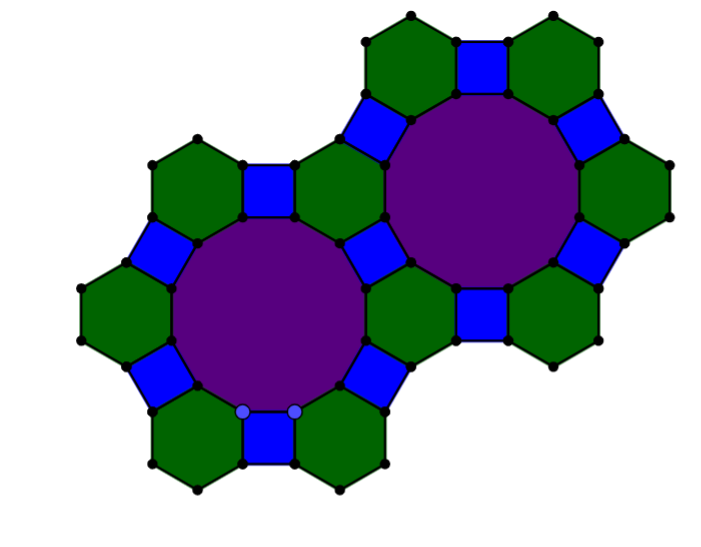
- Dodecagons & Squares & Hexagons
See this article for more on the notation introduced in the problem, of listing the polygons which meet at each point.

