Semi-regular Tessellations
Semi-regular tessellations combine two or more different regular polygons to fill the plane. Can you find all the semi-regular tessellations?
Problem
Semi-regular Tesselations printable sheet
Printable sheets - copies of polygons with various numbers of sides 3 4 5 6 8 9 10 12
Regular tessellations use identical regular polygons to fill the plane. The polygons must line up vertex to vertex, edge to edge, leaving no gaps.
Can you convince yourself that there are only three regular tessellations?
Semi-regular tessellations (or Archimedean tessellations) have two properties:
- They are formed by two or more types of regular polygon, each with the same side length
- Each vertex has the same pattern of polygons around it.
Explore semi-regular tessellations using the Tessellation Interactivity below.
If you've never used the interactivity before, there are some instructions and a video.

The picture shows an arrangement of equilateral triangles and squares. It looks like there's room for another triangle to fill the gap at the top... but can you prove it will fit?
If we tiled the plane with this pattern, we can represent the tiling as {3, 4, 3, 3, 4}, because round every point, the pattern "triangle, square, triangle, triangle, square" is followed. What would the pattern look like if you changed this order?
Can you find all the semi-regular tessellations?
Can you show that you have found them all?
To help you when you are working away from the computer, click below for multiple copies of the different polygons. You can print them, cut them out and use them to test which polygons fit together: 3 4 5 6 8 9 10 12
Getting Started
Here are a couple of methods you could use to work out the interior angles of a regular nine-sided polygon (a nonagon):
1.
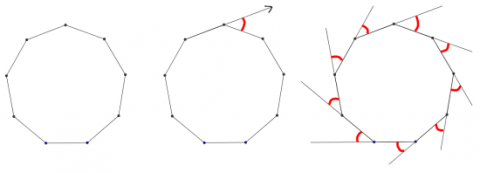
Imagine taking a walk around a regular nine-sided park.
The second picture shows the angle you need to turn through when you reach the first corner.
The third picture shows all the angles you turn through when you walk once round the park.
What angle do you turn through altogether?
What must each exterior angle (the red angles) be?
What must each interior angle be?

2. Here is a regular nonagon:
It has been divided into nine isosceles triangles.
What is the total of all the angles in all the triangles?
Now subtract the angles at the centre of the nonagon to work out the total of all the interior angles of the nonagon.
What must each interior angle be?
Can you adapt these methods for any regular polygon?
Student Solutions
Goeun from Bangok Patana School in Thailand sent in this solution, which includes 8 semi-regular tesselations. Can Goeun be sure to have found them all?
Firstly, there are only three regular tessellations which are triangles, squares, and hexagons. To make a regular tessellation, the internal angle of the polygon has to be a diviser of 360. This is because the angles have to be added up to 360 so it does not leave any gaps. For example, we can make a regular tessellation with triangles because 60 x 6 = 360.
Students from Cowbridge Comprehensive School in Wales used this spreadsheet to convince themselves that only 3 polygons can make regular tesselations.
Goeun continued:
We can prove that a triangle will fit in the pattern {3, 4, 3, 3, 4} [given in the problem] because 360 - (90 + 60 + 90 + 60) = 60 which is the internal angle for an equilateral triangle.
There are 8 semi-regular tessellations in total. We know each is correct because again, the internal angle of these shapes add up to 360.
For example, for triangles and squares, 60 $\times$ 3 + 90 $\times$ 2 = 360.
- Triangles & Squares
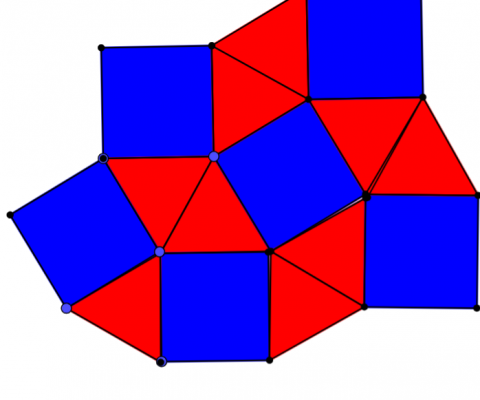
- Triangles & Squares (but a different pattern)

- Hexagons & Triangles
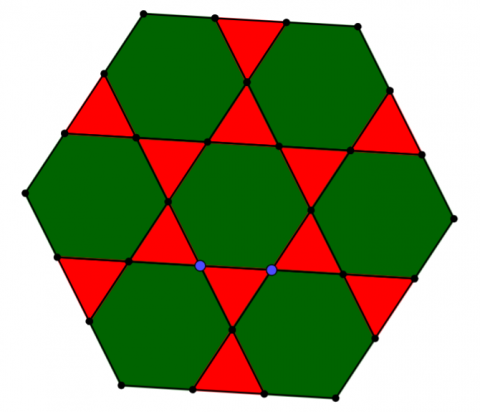
- Hexagons & Triangles (but a different pattern)
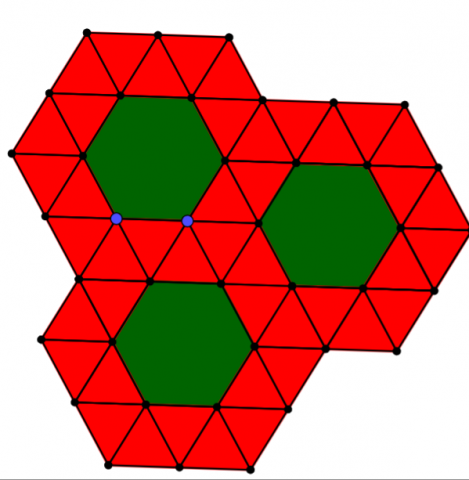
- Hexagons & Triangles & Squares

- Octagons & Squares
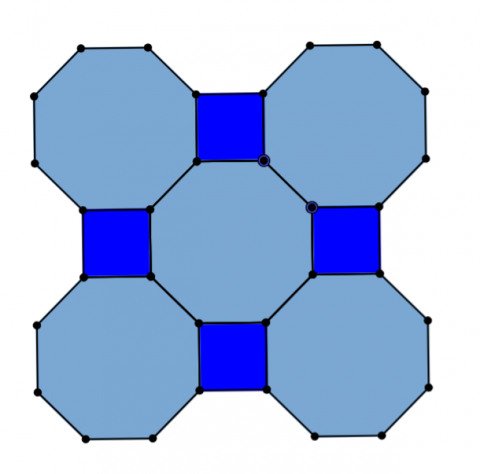
- Dodecagons & Triangles

- Dodecagons & Squares & Hexagons

See this article for more on the notation introduced in the problem, of listing the polygons which meet at each point.
Teachers' Resources
Why do this problem?
Tessellations are a fascinating topic that students of all ages find intriguing. The real world applications of tiling and the opportunity for creating beautiful patterns provide a hook to engage students and stimulate their curiosity, while the interactive environment allows them to quickly test out ideas and make conjectures.
Finding all the possible tessellations provides a context for students to practise working out interior angles of polygons and angles around a point.
Possible approach
Introduce the interactivity to the class, and ask them to consider which shapes you might choose if you wanted to tile an area (with just one type of shape) without leaving any gaps or overlaps.
Ask the students for suggestions or show them this image:

Three equilateral triangles plus two squares gives 60+60+60+90+90=360$^{\circ}$.
Then introduce the notation describing the polygons around each vertex - {3, 4, 3, 3, 4} for the example above.
Key questions
Why do some shapes fit together and others don't?
Possible support
Students could begin by exploring tessellation of quadrilaterals, paying particular attention to the angle properties.
Possible extension
Can students explain why some patterns work around a point but don't tile the area? For example, the decagons and pentagons suggested above. Challenge students to find other similar examples (which could use polygons with more than 12 sides, such as {18, 9, 3}).
Suggest students read Shaping up with Tessellations.
Move on to three dimensions: Which Solids Can We Make?
