Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Semi-regular Tessellations
Age 11 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Here are a couple of methods you could use to work out the interior angles of a regular nine-sided polygon (a nonagon):
1.
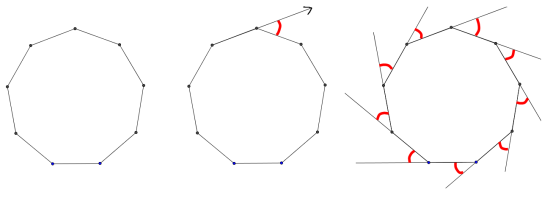
Imagine taking a walk around a regular nine-sided park.
The second picture shows the angle you need to turn through when you reach the first corner.
The third picture shows all the angles you turn through when you walk once round the park.
What angle do you turn through altogether?
What must each exterior angle (the red angles) be?
What must each interior angle be?
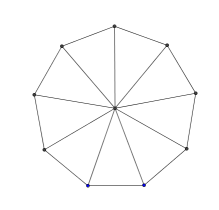
2. Here is a regular nonagon:
It has been divided into nine isosceles triangles.
What is the total of all the angles in all the triangles?
Now subtract the angles at the centre of the nonagon to work out the total of all the interior angles of the nonagon.
What must each interior angle be?
Can you adapt these methods for any regular polygon?

