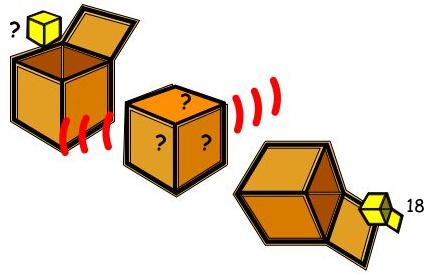
What was in the box?
Problem
What Was in the Box? printable sheet
In the picture below, a number is being put into the box. Inside the box, something happens to the number, and then a new number is tipped out of the box.
The first time this happens, 10 is put into the box. What happens inside the box to get the number 18?
Now three more numbers go into the box, one at a time. The box does the same thing that it did before, and the numbers that are tipped out of the box are:
12
8
15
What were the three new numbers that went in? Remember that the same thing as before happened to all three of those numbers.
-----------
Next, the box does something different to before. Four new numbers are put into the box, one at a time. One of these numbers is 10 and the rest are secret. Something happens inside the box, and the numbers that are tipped out are:
0
19
1
11
What could have happened inside the box? The same thing has happened to all four numbers that went in.
What could the four numbers have been that went into the box?
Are there any other possibilities? How do you know?
Getting Started
Remember, each of the four numbers that goes in has the SAME number added by the big box.
Student Solutions
We did not have many solutions sent in showing their thoughts and recording, but here are a few. This first one came from Michael at Cloverdale Catholic School in Canada:
The number that was put into that box was 10, and out came 18. So, therefore, that wonderful big box added 8. (10 + 8 = 18)
Four other boxes were put into that bigger box, and out popped these numbers: 12, 8, 15 and 10. If the box added eight onto ten to make eighteen, then the other numbers must have been added from eight. How do you figure that out? You use the opposite operation, in which in this case it is addition, so we use subtraction. (12-8=4, so 4+8=12) and (8-8=0, so 0+8=8) and etc.
For the other box, one of the boxes that went into the bigger box was 10, and out came the numbers: 0, 19, 1 and 11. If the number 10 was put in and became the number 0, then 10 was subtracted from 10. Thus, 10-10=0, 29-10=19, 11-10=1, and 21-10=11. If 10 became 19, then 9 was added onto ten. Thus, 10+9=19, (-9)+9=0, (-8)+9=1, and 2+9=11. (A more advanced solution would have been multiplying by 1.9, in which case the numbers before the big box would be 0, 10, ≈0.526 (which means almost 0.526) and ≈5.789.)
There are two possible ways ten could have turned into one: dividing by 10, or subtracting by 9. In division's case: 10÷10=1, 0÷10=0, 190÷10=19, and 110÷10=11. In subtraction's case: 10-9=1, 9-9=0, 28-9=19, and 20-9=11. If 10 was put in that bigger box and became 11, then one was added to ten. Thus, 10+1=11, (-1)+1=0, 18+1=19, and 0+1=1. (An advanced solution is to multiply by 1.1, in which the numbers before the bigger box would have been, ≈17.27, ≈0.9 and 10.)The next one is from Lisa at the Tokyo International School in Japan:
First you have to choose what number/numbers to minus or plus then you choose what box should start with the number. I choose to minus nine in all the boxes. The numbers that come out are 0, 19, 1, 11.
I know that if you take away 9 from ten you get 1. Then you just have to add nine to the rest of the numbers. The number that you get that's the number that you start with. So if you choose to take away the number 9 your solution is 9-9, 28-9, 10-9, 20-9.
Lastly from Louis at the International School, Seychelles:
Minette, Freddie, Ursie from Grandtully Primary in Scotland sent in the following:
We kept the number 10 in our heads, if it was a smaller number we knew it was a take away answer and if it was a bigger number we knew it was an add up.
So once we knew if it was a take away or an add up we kept the 10 in our heads and then we counted from 10 to the number it was going to end with and how many that was.
Then that was what happened in the box!
First the box took away 10 to become 0
Then the box added on 9 to become 19
Then the box took away 9 to become 10
Finally the box added on 1 to become 11
Well done those of you who sent in your ideas to solve this challenge, I wonder how many of you went on to have a look at What's in the Box?
----------------
Teachers' Resources
What Was in the Box?
A number in a little box is put into a wonderful big box that adds something to the number and then a new number comes out at the end:
The first time this happens, 10 is put into the little box, so what happened in the big box to get the answer in the picture above?
Now three more boxes with new numbers in, go into the wonderful box one at a time. It still does the same as before.
So, what were these three new numbers that went in and do you have a better idea of what has been going on - remember it was the same for all four numbers that went in.
-----------
Imagine four new boxes now (with new numbers in) and the wonderful box does a new and different add or take away this time. For one of these boxes the number 10 was put in. The numbers that come out are these:
What could have happened? How did you work these out?
Discuss with others and see if there were different ways that you found the answers.
Why do this problem?
Of course this problem is rather like a function machine, but it can be more interesting and is easily extended to challenge a wide range of pupils. It could be used to introduce children to the idea of addition and subtraction, and offers great opportunities for learners to record in different ways.
Possible approach
Once learners have had some time to work on the first part of the problem in pairs, ask them to share their ways of working with the whole group. Look out for those who give good reasons for choosing particular methods.
You may also like to draw attention to different methods of recording that you observe. Some children may have drawn pictures whereas others may have created calculations.
Key questions
Possible extension
Pupils who are tackling multiplication and division might like to have a go at What's in the Box?.
Possible support