Tunnel vision
How wide is this tunnel?
Problem
A tunnel is cut through a hillside, with a semi-circular cross-section.
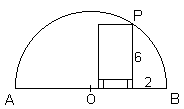
A truck of height 6 m can just drive with its nearside wheels 2 m from the point where the curved roof meets the horizontal road surface.
How wide is the tunnel?
Student Solutions
Using a circle theorem
Triangle ABP is right-angled at P, because a triangle in a semicircle is always right-angled.
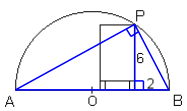
Both of the two smaller right-angled triangles share an angle with triangle ABP, so the three triangles are all similar.
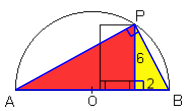
The scale factor between the yellow triangle and the red triangle is 3, so the horizontal side of the red triangle is 6$\times$3=18 m. So the total width of the tunnel is 20 m.
Using Pythagoras' Theorem
OP and OB are both radii, labelled $r$, so the distance from O to the far wheel of the lorry is $r-2.$

Applying Pythagoras' theorem to the right-angled triangle formed, $$\begin{align}r^2=&(r-2)^2+6^2\\
\Rightarrow r^2=&r^2-4r+40\\
\Rightarrow 0=&-4r+40\\
\Rightarrow 4r=&40\\
\Rightarrow r=&10\end{align}$$ So the width of the tunnel is $20$ m.
