Triangles to tetrahedra
Problem
Triangles to Tetrahedra printable sheet
|
Image
Small equilateral |
Image
Isosceles |
|
Image
Right angled isosceles |
Image
Large equilateral |
The sides of the small equilateral triangle are the same length as the short side of the isosceles triangle and the short sides of the right-angled isosceles triangle.
The sides of the large equilateral triangle are the same length as the long sides of the isosceles triangle and the long side of the right-angled isosceles triangle.
You have an unlimited number of each type of triangle.
How many different tetrahedra can you make? Convince us you have found them all.
Images reproduced with kind permission from Polydron.
Getting Started
Think about how the lengths of sides of the triangles are important.
You could use Polydron (plastic shapes that click together) to make the models yourself.
Student Solutions
Students attending a masterclass at the Thomas Deacon Academy in Peterborough tried to work on this problem systematically. Here are examples of how they went about it.
I think their ideas are excellent and give an insight into how you might make a convincing argument that you have all possibilities. Well done to you all for trying to describe your approaches to this problem.
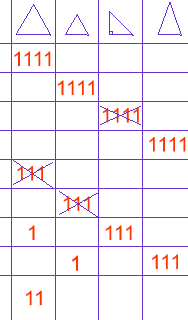
Susannah, Adam, Maria and Erin adopted an approach like the one illustrated in this table. Can you see how they have been systematic and continue their argument? Thanks for this neat idea .
Stephen, Hugh, Daniel and Deepak, adopted a similar approach. Firstly, they identified and coded each of the four triangles, identifying the long and the short sides of each. Then they considered sets of four triangles in a systematic way. Can you see how they worked systematically from the table below:
All the same E,E,E,E SE,SE,SE,SE I,I,I,I R,R,R,R - no 3 and 1 E,E,E,SE- no E,E,E,I - no E,E,E,R-no SE,SE,SE,E - no SE,SE,SE,I -no SE,SE,SE,R-no I,I,I,E - no I,I,I,SE I,I,I,R - no R,R,R,E R,R,R,SE - no R,R,R,I - no 2 and 2 ... ... ...
Emily, Clara, Lizzie and Kieran chose an approach using some further ideas to help them be more efficient:
- There are only two lengths of sides (long, as in the length of the sides of the large equilateral triangle and the hypotenuse of the right-angled triangle; short, as in the length of the sides of the small equilateral triangle and the short side, or base, of the isosceles triangle).
- There must be an even number of long and and even number of short sides in the sets of four triangles that form the tetrahedron if the triangles fit together.
- The even number of sides have to be spread across the triangles, for example four shorts are no good if three of them are all on a small equilateral triangle.
| Even number of longs and shorts/does it work? | ||||
| I | I | I | I | YES/YES |
| EB | EB | EB | EB | YES/YES |
| ES | ES | ES | ES | YES/YES |
| R | R | R | R | YES/NO |
| EB | EB | EB | I | NO |
| EB | EB | EB | ES | NO |
| EB | EB | EB | R | NO |
| I | I | I | ES | YES/YES |
| I | I | I | R | NO |
| I | I | I | EB | NO |
| R | R | R | I | NO |
| R | R | R | ES | NO |
| R | R | R | EB | YES/YES |
| ES | ES | ES | I | YES/NO |
| ES | ES | ES | EB | NO |
| ES | ES | ES | R | NO |
| EB | EB | I | I | YES/YES |
| EB | EB | I | ES | YES/NO |
Other solutions we have received included one from Mark Johnson, who found tetrahedra that use these triangles:
1 small equilateral 3 isosceles
1 big equilateral 3 right-angled
2 big equilateral 2 isosceles
4 small equilateral
4 big equilateral
2 small equilateral 2 right-angled
2 isosceles 1 right-angled 1 big equilateral
2 isosceles 2 right-angled (two different arrangements produce tetrahedra that are reflections of each other )
Yanqing from Lipson Community College can add one more to Mark's list :
1 small equilateral 1 isosceles 2 right-angled
Altogether we have found a total of 10 different tetrahedra.
Teachers' Resources
Why do this problem?
This problem involves using practical equipment to approach a mathematical problem.
It challenges the usual misconception that all tetrahedra are regular.
It needs systematic thinking and visualisation and has some surprises in it - there are a few examples that are quite unexpected.
It is hard to be convinced that you have found all the possibilities and difficult to make the distinction between the two tetrahedra that are mirror images of one another.
Possible approach
- two are isoceles and the other two are equilateral
- one triangle has a right angle
- the triangles have sides of only two possible lengths.
Key questions
How are you recording your findings?