Totality for two
Problem
Here's a game to play with an adult!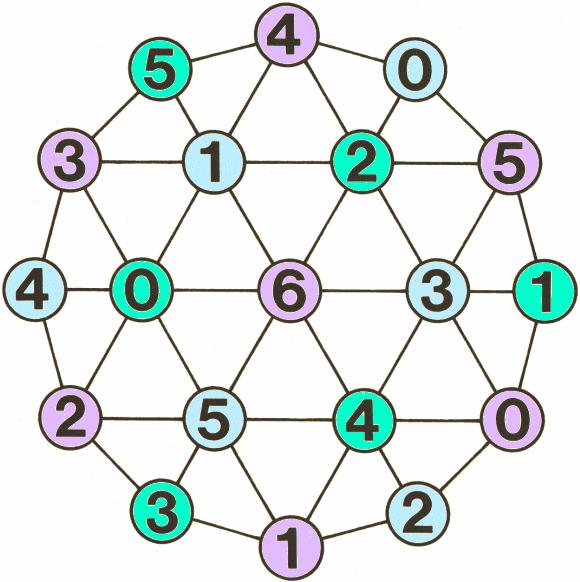
How do you play?
You'll need an adult to play with.
You'll also need a copy of the game board and a counter.
Have a go at working out how to play by watching the video, which has no sound, and discussing what you think the rules are.
You could watch this video, which does have sound, to check the rules:
If you cannot view the videos, you could reveal the rules of the game below:
Slide the shared counter across several adjacent numbers, adding them up as you go to make a 'running' total. Be the player to make the final slide so that the chosen target is reached exactly. Making the total go above the target loses you the game.
How to play:
1. Choose a target to reach. This is the total both you and the adult are trying to make.
2. The adult places their counter on the game board over one of the numbers and says that number.
3. Move the same counter in any direction along a line segment to a neighbouring number and announce the total of the two numbers.
4. The adult moves the same counter to cover a neighbouring number, adds on that number, and announces the 'running' total of the three numbers.
5. Take it in turns to slide the counter to cover a neighbouring number and to add that number to the 'running' total.
6. Players must move when it is their turn.
7. No 'jumping' is allowed.
This game is designed to help children practise number bonds and addition. There is also an opportunity for thinking strategically by working out what will happen several moves in advance.
Easier version: instead of playing against each other, you could work together to try to make 20.
Harder version: discuss what the shortest 'string' of numbers would be that adds to the total. How many different 'strings' of numbers add to that total?
There's a group version of this game here.
