Street party
Problem


The spaces in between the blocks are the roads running North/South and East/West.
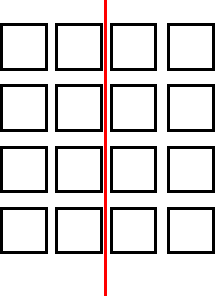
In this town, there are going to be two different parties on the same day which they want to keep separate. So they decide that they will put a fence down the middle of some roads to divide the town up into two equal parts. Because there is 16 block of buildings altogether we'll have to have 8 blocks in each half. Each of the two 8 blocks needs to be kept together with no block being separated
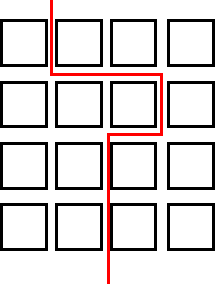
from the rest of that group. So here are two examples that work but the third one does not as it separates the 16 into 3 (not 2) areas.



Well, you can probably guess that the challenge is to find as many routes as you can for the fence to go so that the town is divided up into to halves, each with 8 blocks of course!
Find some good interesting ways of recording the different fence-routes you find.
When you've done a few there may be some things that you want to say about how you are finding the different routes and you may be able to prove that you've found them all! It's good to write such ideas down and when you send in your results make sure that you include the writing. [Don't worry about wonderful sentences or spelling!]
It's probably time to ask the usual question:- "I wonder what would happen if ...?''
a) One child, Michael, recently suggested that it would be interesting to find out what would happen if there was a road blockage somewhere which meant you could not lay a fence down that bit of the road. It leads to some interesting thoughts and some trial routes.

c) A very obvious question would be; "I wonder what would happen if there were more blocks of houses in the town so that the grid was 6 by 4, maybe, or a bigger square that would be 6 by 6?''
Getting Started
You could use some blocks or cardboard boxes to represent the buildings, and lay them on the floor or on a table. Then you could use string or ribbon to show the route of the fence. You could draw your different arrangements, or perhaps take some photos.
Student Solutions
It is wonderful to receive solutions that show so much thought and effort. Joanne has a really neat way of thinking about patterns with start points for the routes. (Well done!) Natasha has tried to report her work in an organised way and come up with some good "What if...'' questions. Jenny has a nice way of explaining her thinking. Jill tries to look at the investigation in some different ways.
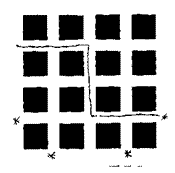
Solution 1, Joanne, West Flegg Middle School
I first thought about the simple routes, for example straight down. That can be changed by going horizontally across the middle.
Then I worked on harder routes. I fund that all regular routes had 4 starting points around the road pattern (without going back over the same route). The irregular pattern of routes had 8 starting points around the road pattern.
In finding this out, I have found out the number of times each route can be used.
The set of road patterns are as follows:
(each map shows one route and all its starting points)
Image

|
Image

|
Image
|
Image

|
Image

|
Image

|
Image

|
Image

|
Image

|
Solution 2, Natasha, West Flegg Middle School
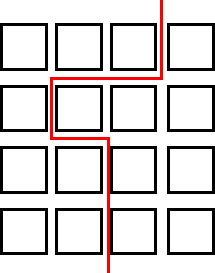
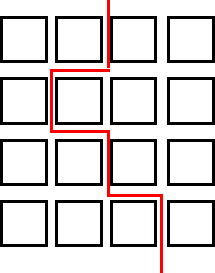
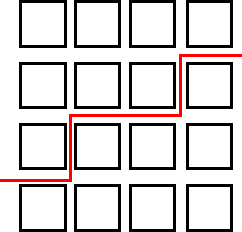
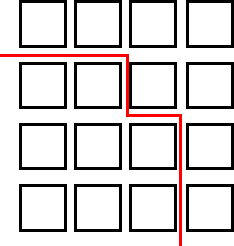
I am finding the routes by picking a square and then just doodling until I find a route that is split into halves (8). Also, by doing the opposite to the one I had done before. I am also drawing a very faint line horizontally - and vertically in pencil, so that I can see roughly where I have to split the street into two. So really what I had to do was divide 16 by 2 = 8.
I had this sudden thought that what if I worked out how many ways I could divide 16 and then I thought maybe I could then prove that I had found them all. But as you can see below, that was definitely not going to work because I only found 2 ways.
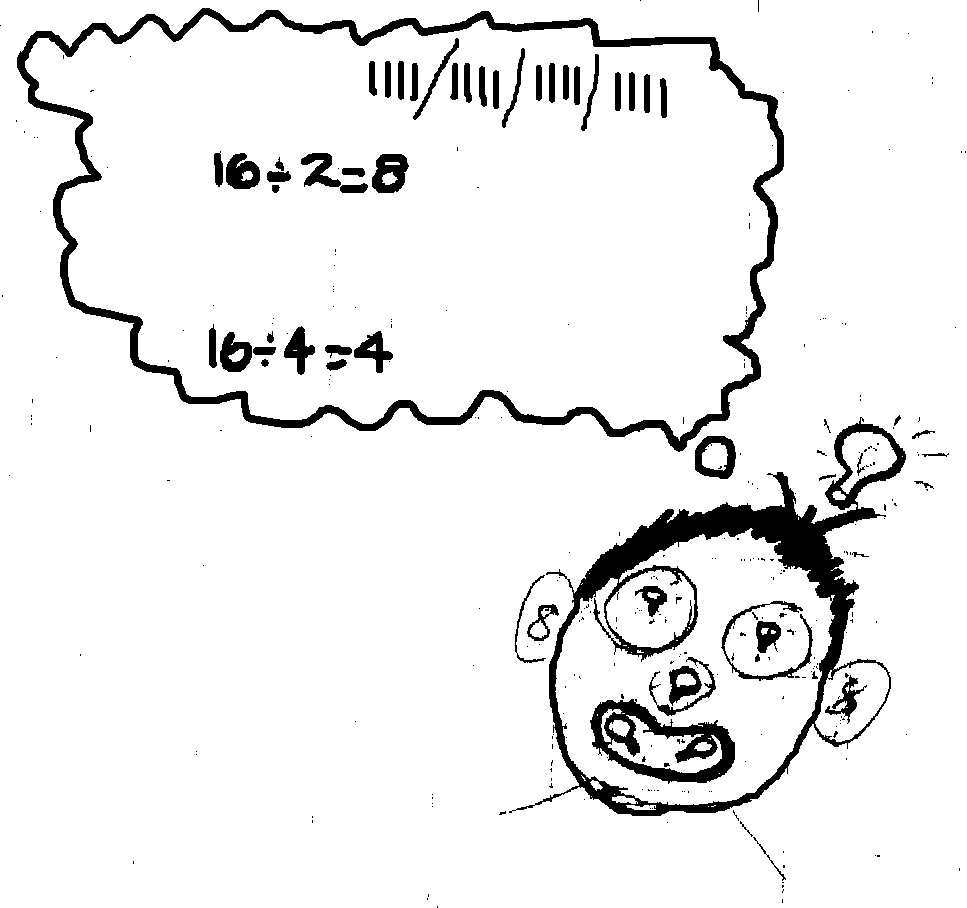
Image

|
Image
|
Image
|
Image
|
Image

|
Image
|
Image
|
Image

|
Image
|
Image
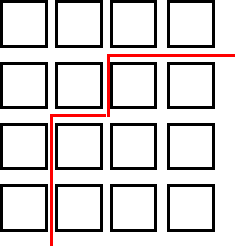
|
| This is as far as I got until I moved on | |
Image
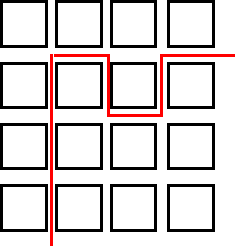
|
Image
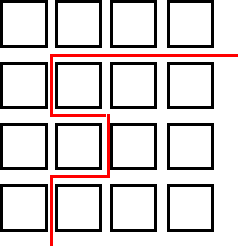
|
My suggestions for "What if''
What would happen if two houses didn't approve of a street party, therefore you wouldn't be able to split the houses (build a fence there?)
Image

|
Image
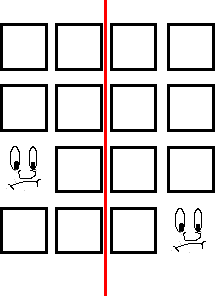
|
Image
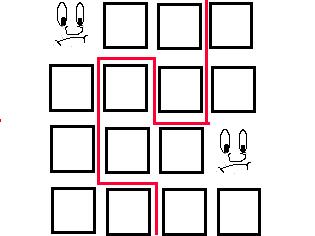
|
Image
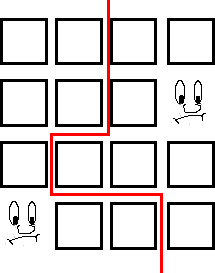
|
What would happen if someone from the street were on holiday and they were coming back on the night of the party and you didn't want to build a fence because you didn't know how they would react.
Image

|
Image
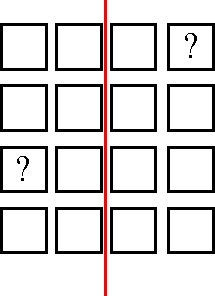
|
Image

|
Image

|
What would happen if you had 49 houses to try and split equally?
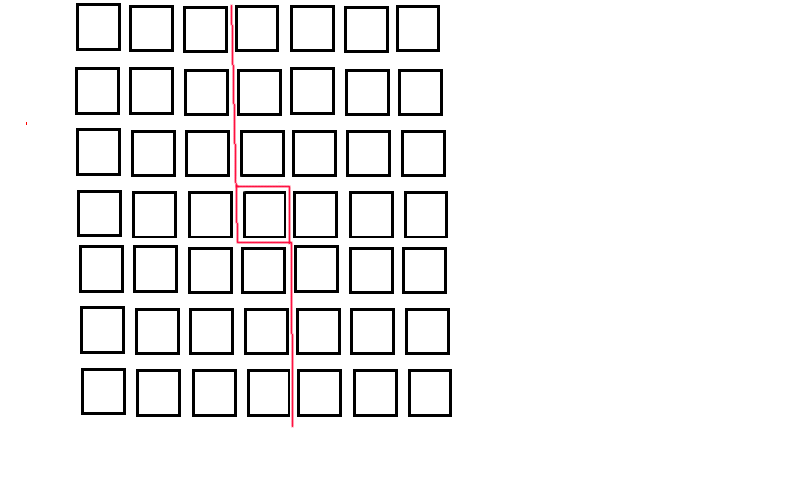
What you would have to do is split the 49 houses into 2 24s that would make 48, then you would have to share the house left over so that you could have 6 hours there each (half of 12 which is the night), or if you were counting it by the whole day (24 hours) 1 street party would use that house 1/4 of the way through the day and have 6 hours and the other party would start 3/4 of the way through.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
Further note
You may be interested in the following talks given by Professor Susan Engels, which focus on encouraging curiosity and are available on YouTube:The Rise and Fall of Curiosity - the extract from 23.50 to 37.15 on adult encouragement and teacher behaviour is particularly worth viewing
The Hungry Mind: The Origins of Curiosity - the extract from 8.22 to 12.29 on children asking questions is especially useful.
