Square grid
Can you work out what fraction of this grid is shaded?
Problem
A square is split into a 100 by 100 square grid.
100 squares in the first row are shaded, 99 in the second row, 98 in the third row, and so on.
What fraction of the whole square is shaded?
This problem is taken from the World Mathematics Championships
Student Solutions
Answer: $\frac{101}{200}$
Notice that there is a total of $100\times100=10 000$ little squares in the grid.
Cutting the grid in half
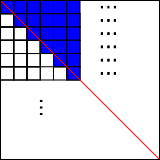
The red line cuts the grid in half.
On each row, there is half of a shaded square on the 'wrong' side of the red line.
So it is $\frac12$ shaded plus $\frac{\frac12}{100}=\frac1{200}$ for the half square per line.
$\frac12 + \frac{1}{200} =\frac{101}{200}$
Adding another row
Add one more row so that the new shape is half shaded:

Grid on right: $100\times101=10 100$ squares, $10 100\div2=5050$ are shaded.
Grid on left: also $5050$ shaded, out of only $10 000$
$\therefore$ fraction shaded is $\frac{5050}{10000}=\frac{101}{200}$
'Counting' the number of shaded squares by making full rows
Move shaded squares to make full rows (and empty rows):
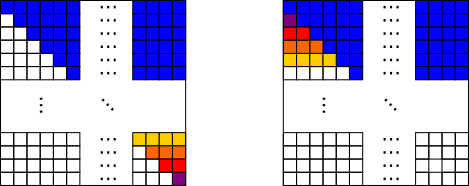
$1$ square is moved into the row with $99$ shaded,
$2$ into the row with $98$ shaded
...
$49$ are moved into the row with $51$ shaded
$50$ are left in the row with $50$ shaded
Total $50\times100+50=5050$ shaded squares (including the row which already had $100$ shaded)
Fraction shaded: $\frac{5050}{10000}=\frac{101}{200}$
