Rough rectangle
What is the smallest possible area that this rectangle could have?
Problem
The length of a rectangle is 6 cm and its width is 5 cm, both correct to the nearest centimetre.
What is the smallest possible area the rectangle could have?
This problem is taken from the World Mathematics Championships
Student Solutions
Answer: 24.75 cm$^2$
Image
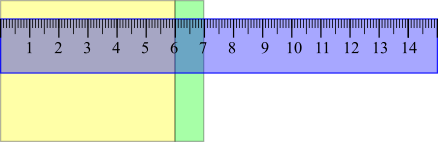
$5.5\le$ length ("6 cm") $\lt 6.5$
Image
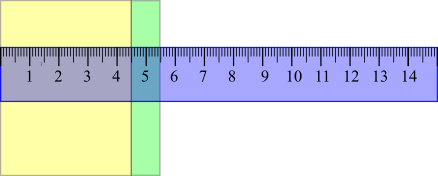
$4.5\leq$ width ("5 cm") $\lt 5.5$
$\therefore$ smallest possible area is $5.5\times4.5=24.75$ cm$^2$
