Room Doubling
Problem
A good friend of mine was telling me about how his house had been changed, part of it was just as simple as this: four square rooms looking a bit like
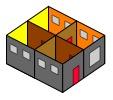

and two walls were taken down so as to make two "double" rooms:


Another way in which it could have been done would look like:-
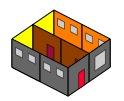

You could make a "model" by using two blocks that are $2$ by $1$ by $1$.

There is nothing particularly exciting about this! But wait ...
We could imagine something a bit larger.
A plan of a building that has six rooms:
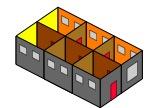

Knocking down walls could make it look like:-
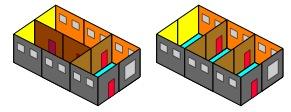


if you were using blocks you might just record it like:-


Maybe we could go to $8$ rooms.
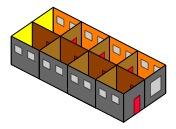

Now we have a lot more examples to explore:-
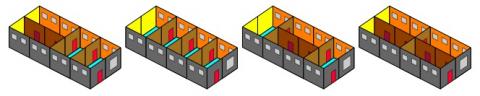




You may also discover:-
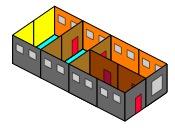

You might say it is the same as the first one. Well it depends what rules you want to make!
The last thing now is to look at making the building have $10$ rooms:-

Some of the results you get might be :-



Well now it is time for you to explore more of your own. You might be using squared paper, blocks that are "two" long, or drawings in which you "rub out" the walls that get knocked down.
The only rules are
- that you start with a rectangular building that is two rooms wide;
- that you only make rooms that are two of the small square rooms put together.
So you probably need to make some record of the ones that you have found. Maybe you do that by drawing, models or numbers.
Well that's all very well.
I hope you got to a $12$-room house.
But you should of course ask "I wonder what would happen if the $12$ rooms were $3$ by $4$ instead of $6$ by $2$?

You might then gets results like :-



but of course there are lots more to find.
Explore and have fun.
The last one I suggest to look at is

with results like :-


It's now up to you to decide what further "I wonder what would happen if....?" questions.
If you draw your results or put down numbers in a table to show many you can find for each number of rooms then you should have something to spend time thinking about. You might then predict how many examples could be found for larger numbers of rooms.
Student Solutions
There are lots of answers to this problem, depending on what questions you choose to ask.
Have a go yourself, and if you discover anything interesting, e-mail us to tell us what you've done! Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried. Teachers - you might like to send in a summary of your children's work.
