Play to 37
This is a game for two players.
Each bag above has unlimited 1s, 3s, 5s or 7s in it.
Aim of the game:
To be the player to add the final number to the 'running' total to make 37.
How to play:
1. Decide who is going first.
2. Player 1 chooses one of the numbers from the bags above (1, 3, 5 or 7).
3. Player 2 then chooses a number from one of the bags and adds this onto Player 1's number to make a 'running' total.
4. Player 1 then has another turn and adds that number onto the 'running' total.
5. Play continues like this with each player choosing a number and adding it onto the 'running' total.
Things to think about:
How many numbers did you use altogether in the game?
Have another go. How many numbers did you use this time?
What is the largest number of numbers you could use to reach 37?
What is the smallest number of numbers you could use to reach 37?
Can you use all the different numbers of numbers in between the largest and the smallest to reach 37?
What do you notice? Will your noticing/s always be true? Can you explain why or why not?
Fran says, "I need to go first in order to win."
Do you agree with Fran? Why or why not?
You may be interested in the other problems in our Problem-solving Classroom Feature.
Thank you to everybody who sent us their solutions to this problem.
Ariana from Halstead Preparatory School in the UK sent in this explanation:
Well done for finding the smallest and largest possible numbers of moves, Ariana! Ariana has worked out that the solution has something to do with the fact that all of the numbers are odd.
Wren from Pierrepont Gamston Primary School in England sent in this explanation:
Well done Wren, we need to use the fact that two odd numbers makes an even number to work out why Player 1 always wins.
Ci Hui Minh Ngoc from Kelvin Grove State College in Brisbane, Australia noticed that the total at the end of Player 1's turn will always be odd, while the total on Player 2's turn will always be even. They sent in this explanation:
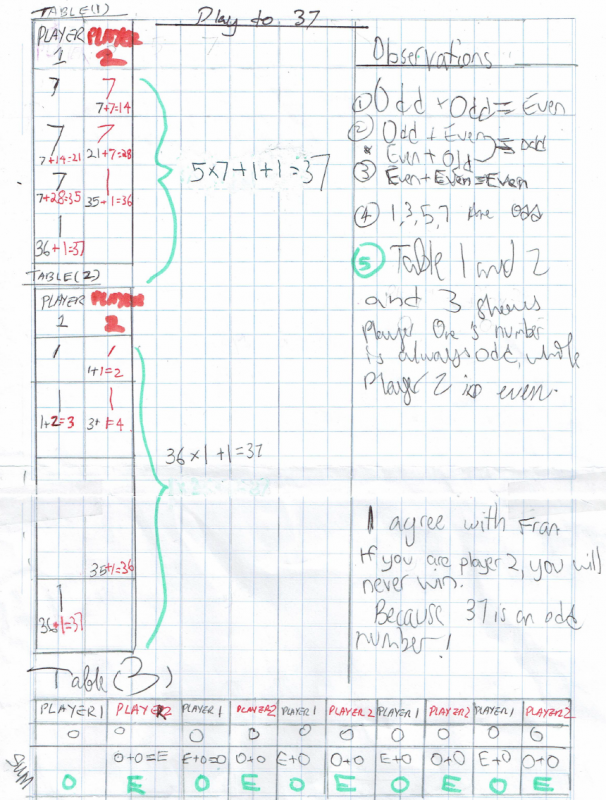
Well done for explaining that, Ci Hui Minh Ngoc - I am now convinced that Player 1 will always win because Player 2 can't get to an odd number on any of their turns.
Ci Hui Minh Ngoc also looked at the different possible numbers of moves. Like Ariana, they found that the lowest number of moves is 7 and the largest is 37. They also found ways of getting to 37 using 9, 13 and 19 moves. I wonder which other numbers of moves are possible between 7 and 37? If you have any ideas about this, please send us an email.
Play to 37
This is a game for two players.
Each bag above has unlimited 1s, 3s, 5s or 7s in it.
Aim of the game:
To be the player to add the final number to the 'running' total to make 37.
How to play:
1. Decide who is going first.
2. Player 1 chooses one of the numbers from the bags above (1, 3, 5 or 7).
3. Player 2 then chooses a number from one of the bags and adds this onto Player 1's number to make a 'running' total.
4. Player 1 then has another turn and adds that number onto the 'running' total.
5. Play continues like this with each player choosing a number and adding it onto the 'running' total.
Things to think about:
How many numbers did you use altogether in the game?
Have another go. How many numbers did you use this time?
What is the largest number of numbers you could use to reach 37?
What is the smallest number of numbers you could use to reach 37?
Can you use all the different numbers of numbers in between the largest and the smallest to reach 37?
What do you notice? Will your noticing/s always be true? Can you explain why or why not?
Fran says, "I need to go first in order to win."
Do you agree with Fran? Why or why not?
You may be interested in the other problems in our Problem-solving Classroom Feature.
Why play this game?
At a basic level, this game provides an opportunity for children to become more fluent in addition. In order to try to win, learners will need to think ahead and this element of strategy demands higher-order thinking. Stepping back to analyse the number of numbers used offers yet more challenge, and the chance to generalise in terms of addition of odd numbers.
Possible approach
This problem featured in the NRICH Primary webinar in June 2022.
Show the picture of the bags of numbers on the interactive whiteboard and explain the rules of the game. You could suggest that you play against the class, or two children could play, or you could split the class in half to play in two teams. Either way, use the board to record the numbers chosen and the running total.
Have another go at the game in this way, again recording the numbers selected and the totals.
Give learners time to play in pairs several times and to record their games as they go along. Then, bring everyone together and ask each pair how many numbers they chose in each game. Record these on the board. Referring to the largest number of numbers and the smallest number of numbers that have been recorded, ask the children whether these are the largest and smallest
possible. Set them off on this challenge and, at a suitable point, open it out into trying to find all the number of numbers in between.
In a plenary, you can record the number of numbers made on the board, all the way from seven (7+7+7+7+7+1+1) up to thirty-seven (thirty seven ones). What do learners notice? Will their noticing/s always be true? Why is this the case?
Key questions
How do you know that you can't use more numbers to make 37?
How do you know you can't use fewer numbers to make 37?
What do the numbers 1, 3, 5 and 7 have in common?
Possible support
Encourage children to use apparatus to help them with the addition if that is where they are struggling. A calculator could be useful if you want them to focus on the analysis rather than the calculations. Learners might like to play Totality before trying this game.
Possible extension
The problem Make 37 follows on nicely from this game and offers an excellent assessment opportunity for you.