Numbered Graph
A weekly challenge: these are shorter problems aimed at Post-16 students or enthusiastic younger students.
Problem
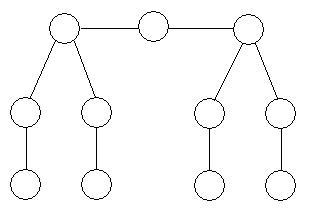
A numbered graph consists of a set of numbered nodes connected by edges. The node sum at a node is the sum of the number at the node and the numbers at all adjacent nodes.
Can you arrange the numbers 1 to 11 on the graph below, using each number exactly once, so the the node sum is the same at each node?
Image
Did you know ... ?
The notion of the mathematical graph is fundamental in modern mathematics and a huge subject of study in its own right. Many systems can be represented by graphs, the internet being a somewhat complicated example. Graph theory is both a fascinating area of pure study and a powerful analytical tool.
The notion of the mathematical graph is fundamental in modern mathematics and a huge subject of study in its own right. Many systems can be represented by graphs, the internet being a somewhat complicated example. Graph theory is both a fascinating area of pure study and a powerful analytical tool.
Student Solutions
We could experiment but let us try to be somewhat systematic.
Since one node will contain the number $11$ and must be connected to at least one other node, the node sum must be at least $12$.
The 'feet' now stand out as the four nodes only connected to one other node. Thus, from the numbers $1, \dots, 11$ we must create 4 pairs with the same sum of at least 12, without repeating any of the numbers.
We thus have the possibility of choosing four pairs from each of the following lines:
(sum 12) (11, 1), (10, 2), (9, 3), (8, 4), (7, 5) leaving (6, *, *) on the top row
(sum 13) (11, 2), (10, 3), (9, 4), (8, 5), (7, 6) leaving (1, *, *) on the top row
(sum 14) (11, 3), (10, 4), (9, 5), (8, 6) leaving (1, 2, 7) on the top row
(sum 15) (11, 4) (10, 5) (9, 6) (8, 7) leaving (1, 2, 3) on the top row
(sum > 15) Impossible to create four pairs.
Since the central node on the top row must have a node sum equal to the sum of the numbers in the top row we see that node sums of 14 and 15 are impossible, as the sum of the numbers in the top row would contradict this.
Furthermore, in the sum 12 case the sum of the two *s must equal 6. This is impossible, as each of the pairs we could use to fill the *s sum to 12.
Furthermore, in the sum 13 case, the sum of the two *s must equal 12. This is impossible, as each of the 5 possible pairs we could use to fill the *s sum to 13.
Therefore it is impossible to number the graph as required.
