The not-so-simple pendulum 2
Things are roughened up and friction is now added to the
approximate simple pendulum
Age
16 to 18
Challenge level
A simple pendulum released from rest from an angle $y$ of less that $20^\circ$ is well-modelled by the linear differential equation
$$m\frac{d^2 y}{dt^2} +k^2y=0\;.$$
Can you work out the meaning of the various letters in the equation, the units of the constant $k$, and find the general solution to this equation?
Look at the solution: it keeps on oscillating for ever. Clearly, this is an unreasonable assumption, as real pendulums stop swinging due to friction.
Here friction is modelled by a force term which is directly proportional to the velocity of the object, acting in the opposite direction to the motion. Do you think that this is a good modelling assumption? What are its strengths and weaknesses?
With this assumption, the differential equation becomes
$$m\frac{d^2 y}{dt^2} + \lambda \frac{d y}{dt}+k^2y=0\;.$$
Can you see how this equation satisfies all of requirements of a motion under friction? What are the units of $\lambda$, and what features of the motion would contribute to it in practice? It is assumed that $\lambda$ is constant: is this a reasonable assumption?
Although this equation might look complicated it is still only a second order differential equation with constant coefficients, so can be solved using standard methods (and a lot of algebra) to give
$$y = \exp\Big[-\frac{\lambda t}{2m}\Big]\Big[A\cos(\Lambda t)+\sin(\Lambda t)\Big] \quad\mbox{and}\quad \Lambda = \sqrt{\frac{k^2}{m}-\frac{\epsilon^2}{4m^2}}\;.$$
Test your skills of differentiation by showing that this equation indeed satisfies the differential equation. More importantly, analyse the solution: how well does it model friction? Consider in particular the amplitude and the frequency of the damped oscillation. Does this meet with your intuitive expectation?
Intuitively, how does friction affect motion? Does the $v$ term
accomplish this to some level?
How does the equation relate to $F=ma$?
As a rough sketch without any calculation, what would you expect the trajectory over time of the exact, real pendulum motion be over time? Compare this to a plot of the solution. What would be realistic values of the parameters? Make some well-reasoned estimations if you have no intuitive sense for the scale of the parameters.
How does the equation relate to $F=ma$?
As a rough sketch without any calculation, what would you expect the trajectory over time of the exact, real pendulum motion be over time? Compare this to a plot of the solution. What would be realistic values of the parameters? Make some well-reasoned estimations if you have no intuitive sense for the scale of the parameters.
We were sent two very impressive solutions to this fascinating problem. We can only assume that Ben from Kenny and Paul (no location given) are going to go on to do great things mathematically!
Both solutions were formatted in careful detail, so we include the two pdf files directly for Paul and Ben. Ben also included his geogebra file for you to have a look at.
Undamped Equation of Motion (with linear approximation)
Image
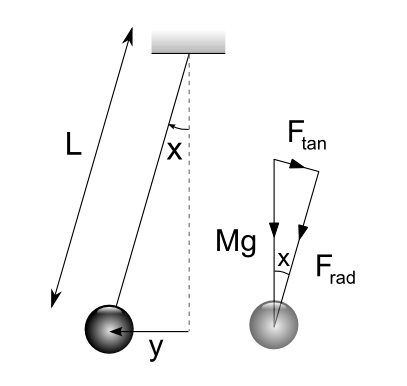
No radial acceleration as $F_{rad}$ balanced by tension in string.
Newton's Second Law:
$$\sum_{i}\mathbf{F_i} = \frac{\textrm{d}}{\textrm{d}t}(m \mathbf{v})\;.$$
Considering the tangential direction:
$$F_{tan} = mg \sin x \quad\textrm{ and }\quad a_{tan} = -\ddot{x} \ell $$
$$\Rightarrow -mg \sin x = m\ddot{x}\ell\;.$$
$\sin x = \frac{y}{\ell}$ from trigonometric definitions $\Rightarrow y = \ell \sin x\;.$
For small $x$ ($x < 20^\circ$ from question), $\sin x \approx x$
$$\Rightarrow y = \ell x \Rightarrow \ddot{x} = \frac{\ddot{y}}{\ell}\;.$$
Substituting:
$$
\begin{align}
mg \frac{y}{\ell} &= -m \frac{\ddot{y}}{\ell} \ell\\
\frac{mg}{\ell}y &= -m\ddot{y}\\
m\ddot{y} + \frac{mg}{l}y &= 0
\end{align}
$$
$\Rightarrow k = \sqrt{\frac{mg}{\ell}}$ with units $\sqrt{\textrm{kg}}\ \textrm{s}^{-1}\;.$
Inclusion of friction (damped response)
Taking the frictional forces acting on the pendulum as being proportional and in opposite direction to the velocity of the bob is a good model in part, reflecting well the drag forces acting on the bob, which at such low velocities do exhibit a proportionality to velocity (Stoke's drag - see Modelling article) and replicating the observed real-life behaviour of decaying amplitude of
oscillations. This model does not however account well for the frictional forces acting at the 'hinge point' of the pendulum as these are likely to be independent of velocity, however as they are also likely to be fairly insignificant in most cases, the model is still valid.
Deriving the equation of motion again using Newton's second law and this time including the drag force (assuming constant of proportionality $\lambda$):
$$-mg \sin x - \lambda \dot{x} \ell = m\ddot{x}\ell\;.$$
Note the signs are important here - acceleration is being taken as positive in the direction of increasing $x$ and so the weight component is negative as it acts in the opposite direction, as is the drag force as it always acts to oppose motion.
As before assuming small $x$, so $\sin x \approx x$ and using $x = \frac{y}{\ell}$:
$$
\begin{align}
-mg \frac{y}{\ell} - \lambda \frac{\dot{y}}{\ell} \ell &= m \frac{\ddot{y}}{\ell} \ell\\
m\ddot{y} + \lambda \dot{y} + \frac{mg}{\ell} y &= 0\\
m\ddot{y} + \lambda \dot{y} + k^2 y &= 0
\end{align}
$$
$$
\begin{align}
-mg \frac{y}{\ell} - \lambda \frac{\dot{y}}{\ell} \ell &= m \frac{\ddot{y}}{\ell} \ell\\
m\ddot{y} + \lambda \dot{y} + \frac{mg}{\ell} y &= 0\\
m\ddot{y} + \lambda \dot{y} + k^2 y &= 0
\end{align}
$$
$\therefore \lambda$ has units $\textrm{kg s}^{-1}$. It will depend on the geometry the pendulum (bob) and properties of the fluid it is moving through. Over the range of velocities that would be expected for a pendulum of reasonable dimensions acting under Earth's gravitational field it is reasonable to assume $\lambda$ would remain constant.
Assuming the solution to the equation has form $y = C e^{pt}$ where $C$ is a constant:
$$m\left(p^2 C e^{pt}\right) + \lambda \left(p C e^{pt}) + k^2 (C e^{pt}\right) = 0\;.$$
Taking non-trivial solutions, i.e. $C \ne 0$ and as in general $e^{pt} \ne 0$:
$$\Rightarrow mp^2 + \lambda p +k^2 = 0$$
$$ p = \frac{-\lambda \pm \sqrt{\lambda^2 - 4(m)(k^2)}}{2m}$$
$$ p = \frac{-\lambda}{2m} \pm \sqrt{\frac{\lambda^2 - 4mk^2}{4m^2}}$$
$$ p = \frac{-\lambda}{2m} \pm \sqrt{\frac{\lambda^2}{4m^2} - \frac{k^2}{m}}\;.$$
Assuming $\lambda^2 < 4mk^2$ i.e. $\lambda^2 < \frac{4m^2g}{\ell}$ (this is likely to be the case in most real life situations and is called under-damping) the roots to the characteristic equation will be complex:
$$ p = \frac{-\lambda}{2m} \pm i\sqrt{\frac{k^2}{m}-\frac{\lambda^2}{4m^2}}$$
$$ \Lambda = \sqrt{\frac{k^2}{m}-\frac{\lambda^2}{4m^2}} \Rightarrow p = \frac{-\lambda}{2m} \pm i \Lambda\;.$$
Therefore the general solution is:
$$y = C \exp \left[ \left( \frac{-\lambda}{2m} + i \Lambda \right) t \right] + D \exp \left[ \left( \frac{-\lambda}{2m} - i \Lambda \right) t \right]\;,$$
$$y = \exp \left[ \frac{-\lambda}{2m} t \right] \left( C \exp \left[ i \Lambda t \right] + D \exp\left[- i \Lambda t \right] \right)\;.$$
Euler's formula $e^{i\theta} = \cos \theta + i \sin \theta$:
$$\Rightarrow y = \exp \left[ \frac{-\lambda}{2m} t \right] \left( C \left[ \cos (\Lambda t) + i \sin (\Lambda t) \right] + D \left[ \cos (-\Lambda t) + i \sin (-\Lambda t) \right] \right)\;.$$
$\cos \theta$ is an even function $\Rightarrow \cos (-\Lambda t) = \cos (\Lambda t)\;.$
$\sin \theta$ is an odd function $\Rightarrow \sin (-\Lambda t) = -\sin (\Lambda t)\;.$
$$
\begin{align}
y &= \exp \left[ \frac{-\lambda}{2m} t \right] \left( C \left[ \cos (\Lambda t) + i \sin (\Lambda t) \right] + D \left[ \cos (\Lambda t) - i \sin (\Lambda t) \right] \right)\;,\\
y &= \exp \left[ \frac{-\lambda}{2m} t \right] \left[ (C+D) \cos (\Lambda t) + i(C-D) \sin (\Lambda t) \right]\;.
\end{align}
$$
Let $A = C + D$ and $B = i(C-D)$:
$$y = \exp \left[ \frac{-\lambda}{2m} t \right] \left[ A \cos (\Lambda t) +B \sin (\Lambda t) \right]\;.$$
Therefore,
$$
\begin{align}
\dot{y} &= \frac{-\lambda}{2m} \exp \left[ \frac{-\lambda}{2m} t \right] \left[ A \cos (\Lambda t)+B \sin(\Lambda t) \right] + \exp \left[ \frac{-\lambda}{2m} t \right]\left[ - \Lambda A \sin (\Lambda t) + \Lambda B \cos (\Lambda t) \right]\\
\dot{y} &= \exp \left[ \frac{-\lambda}{2m} t \right] \left[ \left(\Lambda B - \frac{\lambda}{2m}A \right) \cos (\Lambda t) - \left(\Lambda A + \frac{\lambda}{2m}B \right) \sin (\Lambda t) \right]
\end{align}
$$
and
$$
\begin{align}
\ddot{y} &= \frac{-\lambda}{2m} \exp \left[ \left(\Lambda B - \frac{\lambda}{2m}A \right) \cos (\Lambda t) - \left(\Lambda A + \frac{\lambda}{2m}B \right) \sin (\Lambda t) \right] + \\
& \qquad \exp \left[ \frac{-\lambda}{2m} t \right] \left[ -\Lambda \left(\Lambda B - \frac{\lambda}{2m}A \right) \sin (\Lambda t) - \Lambda \left(\Lambda A + \frac{\lambda}{2m}B \right) \cos (\Lambda t) \right]\\
\ddot{y} &= \exp\left[ \frac{-\lambda}{2m} t \right] \left[ \left( \left( \frac{\lambda}{2m} \right)^2 A - 2 \left( \frac{\lambda}{2m} \right) B - \Lambda^2 A \right) \cos (\Lambda t)\right. + \\
& \qquad\left.\left( \left( \frac{\lambda}{2m} \right)^2 B + 2 \left( \frac{\lambda}{2m} \right) A - \Lambda^2 B \right) \sin (\Lambda t) \right]
\end{align}
$$
Substituting back in to $ m\ddot{y} + \lambda \dot{y} + k^2 y = 0$ gives:
$$
\begin{align}
0 =
& m \left\{
\exp \left[ \frac{-\lambda}{2m} t \right] \left[ \left( \left( \frac{\lambda}{2m} \right)^2 A - 2 \left( \frac{\lambda}{2m} \right) B - \Lambda^2 A \right) \cos (\Lambda t) + \right.\right.\\
&\qquad\left.\left.\left( \left( \frac{\lambda}{2m} \right)^2 B + 2 \left( \frac{\lambda}{2m} \right) A - \Lambda^2 B \right) \sin (\Lambda t) \right]
\right\} + \\
& \qquad\lambda \left\{
\exp \left[ \frac{-\lambda}{2m} t \right] \left[ \left(\Lambda B - \frac{\lambda}{2m}A \right) \cos (\Lambda t) - \left(\Lambda A + \frac{\lambda}{2m}B \right) \sin (\Lambda t) \right]
\right\} + \\
& \qquad k^2 \left\{
\exp \left[ \frac{-\lambda}{2m} t \right] \left[ A \cos (\Lambda t) +B \sin (\Lambda t) \right]
\right\}
\end{align}
$$
$$
\begin{align}
0 = \exp \left[ \frac{-\lambda}{2m} t \right]
& \cos (\Lambda t)
\left\{
m \left(\frac{\lambda}{2m}\right)^2 A - 2m \left(\frac{\lambda}{2m}\right) \Lambda B - m \Lambda^2 A + \right.\\
&\qquad\qquad\left.\lambda \Lambda B -\lambda \left(\frac{\lambda}{2m}\right) A + k^2 A
\right\} +
\\
& \sin (\Lambda t)
\left\{
m \left(\frac{\lambda}{2m}\right)^2 B + 2m \left(\frac{\lambda}{2m}\right) \Lambda A - m \Lambda^2 B - \right.\\
&\qquad\qquad\left.\lambda \Lambda A -\lambda \left(\frac{\lambda}{2m}\right) B + k^2 B
\right\}
\end{align}
$$
$$
\begin{align}
0 = \exp \left[ \frac{-\lambda}{2m} t \right]
& \cos (\Lambda t)
\left\{
\left(\frac{\lambda^2}{4m}\right) A - \lambda \Lambda B - m \left( \frac{k^2}{m}-\frac{\lambda^2}{4m^2} \right) A + \right.\\
&\qquad\qquad\left.\lambda \Lambda B -\left(\frac{\lambda^2}{2m}\right) A + k^2 A
\right\} +
\\
& \sin (\Lambda t)
\left\{
\left(\frac{\lambda^2}{4m}\right) B + \lambda \Lambda A - m \left( \frac{k^2}{m}-\frac{\lambda^2}{4m^2} \right) B - \right.\\
&\qquad\qquad\left.\lambda \Lambda A - \left(\frac{\lambda^2}{2m}\right) B + k^2 B
\right\}
\end{align}
$$
$$ \begin{align}
0 = \exp \left[ \frac{-\lambda}{2m} t \right]
& \cos (\Lambda t)
\left\{
\left(\frac{\lambda^2}{4m}\right) A - k^2 A + \left( \frac{\lambda^2}{4m} \right) A -\left(\frac{\lambda^2}{2m}\right) A + k^2 A
\right\} +
\\
& \sin (\Lambda t)
\left\{
\left(\frac{\lambda^2}{4m}\right) B - k^2 B + \left(\frac{\lambda^2}{4m} \right)B - \left(\frac{\lambda^2}{2m}\right) B + k^2 B
\right\}
\end{align}
$$
$$ 0= \exp \left[ \frac{-\lambda}{2m} t \right]
\cos (\Lambda t) \left\{ \left(\frac{\lambda^2}{2m}\right) A - \left(\frac{\lambda^2}{2m}\right) A \right\}
+ \sin (\Lambda t) \left\{ \left(\frac{\lambda^2}{2m}\right) B- \left(\frac{\lambda^2}{2m}\right) B \right\}$$
$$ 0 = \exp \left[ \frac{-\lambda}{2m} t \right] \cos (\Lambda t) \left\{ 0 \right\} + \sin (\Lambda t) \left\{ 0 \right\} = 0$$
$\therefore$ solution is valid.
Taking initial conditions $y(0) = Y_0$ and $\dot{y}(0) = 0$:
$$
\begin{align}
y(0) = Y_0 \Rightarrow & Y_0 = \exp(0) \left[ A \cos (0) +B \sin (0) \right]\\
& Y_0 = (1) \left[ A (1) +B (0) \right] \\
& A = Y_0\\
\end{align}
$$
$$
\begin{align}
\dot{y}(0) = 0 \Rightarrow & 0 = \exp(0) \left[ \left(\Lambda B - \frac{\lambda}{2m} Y_0 \right) \cos (0) - \left(\Lambda Y_0 + \frac{\lambda}{2m}B \right) \sin (0) \right]\\
& 0= (1) \left[ \left(\Lambda B - \frac{\lambda}{2m} Y_0 \right) (1) - \left(\Lambda Y_0 + \frac{\lambda}{2m}B \right) (0) \right] \\
& B = \frac{\lambda Y_0}{2m \Lambda}\\
\end{align}
$$
$$\therefore y = \exp \left[ \frac{-\lambda}{2m} t \right] \left[ Y_0 \cos (\Lambda t) + \frac{\lambda Y_0}{2m \Lambda} \sin (\Lambda t) \right]$$
Why do this problem?
This
problem takes the equation for simple harmonic motion to the
next stage of complexity. The solution to the equation is provided
giving students an opportunity to explore the interpretation of an
equation/solution and to see where calculus might start to go at
university.
Possible approach
There are three obvious ways in which this problem could be
used:
First way: As a
discussion point into modelling assumptions, work with the solution
as given. This would work in any context in which students are
beginning to develop an understanding of differentiation equations.
This particular equation is interesting because it offers a
reasonable level of complexity whilst still allowing for a solution
involving only simple functions.
Start by discussing friction. How does this affect motion? Why
is the $v$ term a sensible candidate for modelling this? How does
the equation relate to $F=ma$?
Next discuss the expected qualitative form of a damped
pendulum motion. Then proceed to look at the form of the solution
to see if it compares with this. At one level, the solution might
clearly be seen both to decay and oscillate, but more detail will
be needed to see if the decay occurs at a sensible rate. Students
will need to choose some sensible values for the parameters in
order to do this. They are unlikely to have any sense of the
appropriate scale for $\lambda$, so might need to try out a range
of values.
Students could try to plot the solution (either numerically,
or as a curve sketching exercise) and show that this would seem to
represent a damped pendulum motion.
Second way: The
solution to this problem is a relatively extended piece of
mathematics. Can students work their way through this? This gives
an excellent revision into concepts from calculus such as chain
rule, product rule and differentiation of standard functions, and
gives a good flavour of the complexities of 1st year undergraduate
mathematics.
Third way: Students
could try to differentiate the solution twice and substitute back
into the equation to show that it works. This would be best tackled
just prior to coming to university: suggest that students
interested in a mathematics or engineering degree work through the
problem to gain insight into what is to come and also to give their
differentiation a solid workout.
Key questions
Intuitively, how does friction affect motion? Does the $v$
term accomplish this to some level?
How does the equation relate to $F=ma$?
As a rough sketch without any calculation, what would you
expect the trajectory over time of the exact, real pendulum motion
be over time? Compare this to a plot of the solution.
What would be realistic values of the parameters? Make some
well-reasoned estimations if you have no intuitive sense for the
scale of the parameters.
Possible extension
This equation is not the final part in the story of modelling
the simple pendulum. Students might try to devise an accurate
experiment to determine its accuracy, or to suggest alternative
forms of the equation with other friction or drag terms in.
Possible support
Try
The Not-So-Simple Pendulum 1 first.