Neighbours
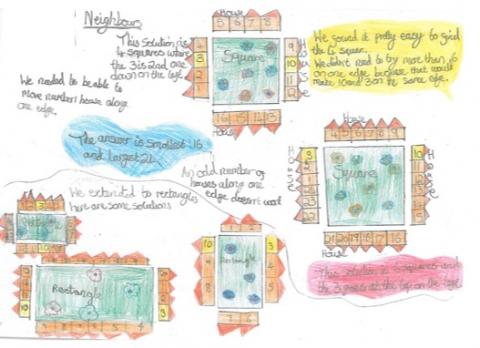
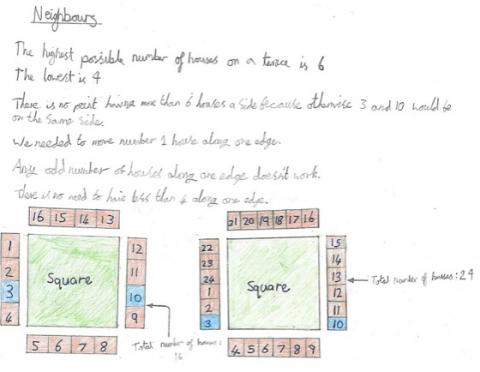
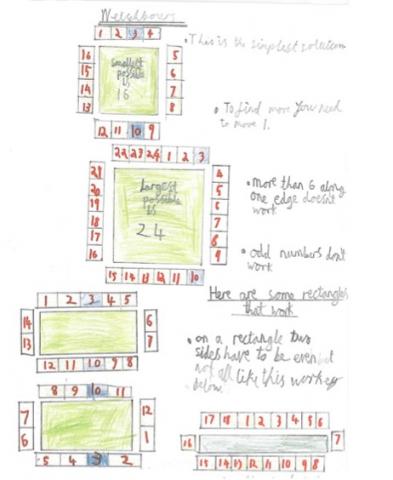
In a square in which the houses are evenly spaced around the outside, numbers $3$ and $10$ are opposite each other.
What is the smallest number of houses in the square?
What is the largest possible number of houses in the square?
Why do this problem?
This problem combines numerical and spatial reasoning. Learners will use basic counting but also an understanding of factors and multiples. It can be approached in many different ways and can therefore lead to discussions about different methods and different representations.
Possible approach
It would be a good idea to introduce this problem orally to the class at first, perhaps showing them the picture of the houses around the square if necessary, which emphasises that there are no houses on the corners. Having explained the challenge, give them a moment to think on their own about how they might tackle the problem, then invite them to share ideas with a partner. After a few
minutes, share some suggestions with the whole group. At this stage, it is important not to make any judgements about the possible ways forward.
Give pairs time to work together on the problem. Have a variety of resources to hand for them to use if they would like, such as squared paper, numbered counters, pencils, plain paper, mini whiteboards ... Give each pair a large sheet of paper too and explain that it is for recording the steps they have taken in order to reach their solution.
After a suitable length of time, display their large sheets on the wall or board, or leave them flat on tables, and give everyone time to read them. Bring the whole group together and invite comments about the different approaches. Did anyone have a good system for working on this problem? What sorts of things did they put on paper and why? Go on to discuss the solution itself. How did the
children know they had got the smallest and largest number of houses? Do they notice a connection between the maximum number of houses on each side of the square and the difference between the two house numbers? Can they explain their observations?
You can challenge them further by asking whether they could predict solutions for house numbers $4$ and $10$ being opposite each other. Give them time to work on this new problem. What is the same about this solution compared with the first challenge? What is different? Can they explain why?
Key questions
If the houses are evenly spaced around the four sides of a square, what do you know about the total number of houses?
We know there is a number $10$ house. What does that tell us about the total number of houses?
Where could house number $1$ go?
Have you thought of drawing a picture?
Possible extension
Encourage learners to explore other combinations of house numbers. How about $17$ and $59$ being opposite each other? Pupils could also ask their own 'what if ...?' questions. For example, what would happen if the houses were arranged in a rectangle rather than a square?
Possible support
Encourage children to sketch pictures to represent the problem. Alternatively, using numbered counters to represent the houses may help them to try out ideas.