Multilink Cubes
Take 36 cubes.
Challenge 1
How many different blocks can you make? For example 6 by 6 by 1, or 3 by 6 by 2.Just how many different ones can you find?
Challenge 2
Try growing different pyramids of cubes which in turn generate different sequences of numbers. Look at the pictures below this table and see if you can work out how the table has been filled in.
| 1 | 2 | 3 | |
| A | 1 | 3 | 5 |
| B | 1 | 4 | 10 |
| C | 1 | 5 | 14 |
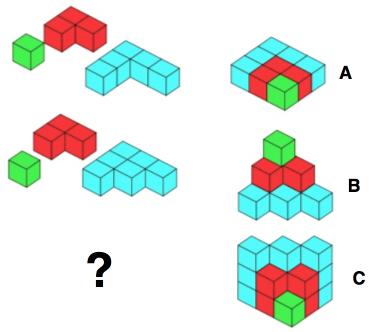
- Can you continue the table?
- What patterns do you notice?
- Can you explain why these patterns occur?
Have a go for yourself, and if you discover anything interesting then let us know!
Multilink Cubes
Take 36 cubes.
Challenge 1
How many different blocks can you make? For example 6 by 6 by 1, or 3 by 6 by 2.Just how many different ones can you find?
Challenge 2
Try growing different pyramids of cubes which in turn generate different sequences of numbers. Look at the pictures below this table and see if you can work out how the table has been filled in.
| 1 | 2 | 3 | |
| A | 1 | 3 | 5 |
| B | 1 | 4 | 10 |
| C | 1 | 5 | 14 |
- Can you continue the table?
- What patterns do you notice?
- Can you explain why these patterns occur?
Why do this problem?
This activity gives pupils the opportunity to explore some simple number relationships, from which they can be encouraged to make some generalisations. It may also be a good context in which to help pupils ask their own questions - "I wonder what would happen if we ...?" pursuing their curiosity. You will be aware that a lot of perseverance is helpful in solving this challenge. Further support regarding nurturing curiosity can be found at the foot of this page.
Possible approach
With younger pupils or those with little experience of exploration in mathematics and talking about their mathematical thoughts, it would be good to certainly start with cubes that they can handle.
It might also be appropriate for you to bring everyone together after some time to discuss how they are going about their exploration and how they are recording their work.
Invite pupils to ask and begin to answer their own questions: "I wonder what would happen if I ...?". You could use some of the suggestions in the problem itself to prompt those who may not be used to doing this.
Key questions
Tell me what you have noticed about the numbers of cubes.
What else are you going to explore?
Tell me about what's going on with other shapes of collections of cubes.
Possible extension
Some pupils might look at generalisations that they can say about different layout at the start of any sequence of cubes.
Possible support
Some pupils may find it helpful to approach the problem using practical equipment, and having help in arranging them.
Further note
You may be interested in the following talks given by Professor Susan Engels, which focus on encouraging curiosity and are available on YouTube:The Rise and Fall of Curiosity - the extract from 23.50 to 37.15 on adult encouragement and teacher behaviour is particularly worth viewing
The Hungry Mind: The Origins of Curiosity - the extract from 8.22 to 12.29 on children asking questions is especially useful.