Just touching
Problem
Image
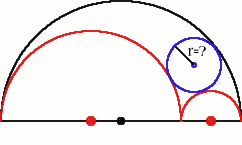
|
Two semi-circles are drawn on one side of a line segment. Another semi-circle touches them externally as shown in the diagram.
What is the radius of the circle that touches all three semi-circles in terms of the radii of the first two semi-circles?
|
Getting Started
Find lengths in terms of the radii of the two red semicircles.
Student Solutions
This solution comes from Sue Liu of Madras College
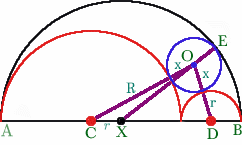
Let the large semi-cirle have diameter $AB$ and centre $X$.
Let the two smaller semi-circles have centres $C$ and $D$ and radii $R$ and $r$.
Thus $AC = R$, $BD = r$ so that $AX = (2R + 2r)/2 = (R + r)$ and $CX = r$ from which it follows that $XD = R$.
Let the small circle have have centre $O$ and radius $x$.
Then $CO = R + x$ and $DO = r + x$.
The line $XO$, joining the centre of the large semicircle to the centre of the small circle, cuts the circumference of the large semicircle at $E$ where $XE = XB = R + r$, $OE = x$ and $OX = R + r - x$.
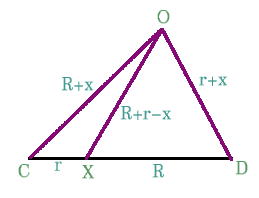
If we now consider the triangle $OCD$ we have
Image
|
|
$\angle OXC + \angle OXD = 180^o$
So
\begin{eqnarray}\frac{r^2 + (R + r - x)^2 - (R + x)^2}{2r(R + r - x)} + \frac{R^2 + (R + r - x)^2 - (r + x)^2}{2R(R + r - x)} = 0\end{eqnarray}
Teachers' Resources
