Hexagon Slices
This regular hexagon has been divided into four trapezia and one hexagon.... what is the ratio of the lengths of sides p, q and r?
This regular hexagon has been divided into four trapezia and one hexagon. If each of the five sections has the same perimeter, what is the ratio of the lengths $p$, $q$ and $r$?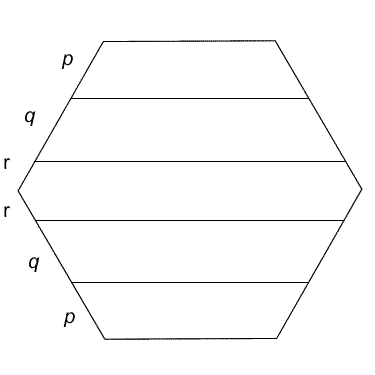 
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
YoeEun Lee, Jinwoo Son, Soyoon Park, Jinho Kim, Kazuharu Nagamura, and Devang Nair, all from the Class of 2024 from the Canadian Academy submitted these three excellent solutions to the problem.
An alternative approach is available below:
Each exterior angle of a regular hexagon is $60^{\circ} (360^{\circ}/6)$, so when sides HB and IC are extended to meet at A , an equilateral triangle, ABC is created.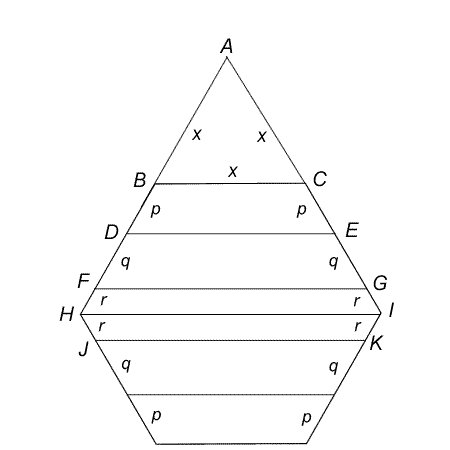
Let the sides of this triangle be of length x. As BC, DE and FG are all parallel, triangles ABC, ADE and AFG are all equilateral. So, DE = DA = $p$ + $x$; and FG = FA = $q$ + $p$ + $x$.
The perimeter of trapezium BCED = $x + p + x + 2p = 2x + 3p$;
The perimeter of trapezium DEGF = $(p + x) + (q + p + x ) + 2q = 2x + 2p + 3q$;
The perimeter of hexagon FGIKJH = $2((q + p + x) + 2r ) = 2x + 2p + 2q + 4r$.
So, $2x$ + $3p$ = $2x$ + $2p$ + $3q$ ; hence $p$ = $3q$.
Also $2x$ + $2p$ + $3q$ = $2x$ + $2p$ + $2q$ + $4r$ ; hence $q$ = $4r$ .
So, $p$ : $q$ : $r$ = $12r$ : $4r$ : $r$ = $12$ : $4$ :$1$