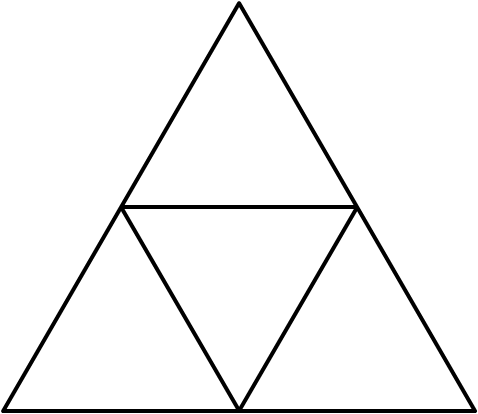
Half and Half
Two of the four small triangles are to be painted black. In how many ways can this be done?
Problem
Image
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Answer: 6
Here are two possible ways of thinking about this problem, although there are many other possibilities.
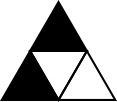
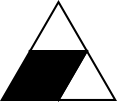
Choosing the colour of the top triangle
Image

Image

Image
Image
Image

Image

$6$ possibilities.
Choosing which triangles are black



If the top triangle is painted black, there are three choices for the other black triangle.
Choosing which triangles are black
Image

Image

Image

Image

Image

Image

This means there are $3+2+1=6$ possibilities.
This problem is looking at the number of ways to choose two of the four triangles to paint black. This can be written as $^4C_2$ or $4 \choose 2$, which are called binomial coefficiants. If you want to find out more about these, then you can look at this article.
