Golden thoughts
Rectangle PQRS has X and Y on the edges. Triangles PQY, YRX and XSP
have equal areas. Prove X and Y divide the sides of PQRS in the
golden ratio.
Problem
Consider the following diagram:
Image
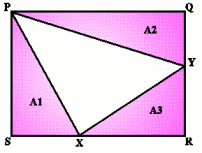
Given that the areas of $A1$, $A2$ and $A3$ in the above diagram are equal, show that $${RX\over XS} = {RY\over YQ} = {{\sqrt{5}+ 1}\over 2}$$ so that the points $X$ and $Y$ divide the sides of the rectangle in the golden ratio.
Getting Started
Let
$PS = x$
$SX= a$
$XR= b$
Can you relate the areas of the triangles using these values?
Student Solutions
Sue from Madras College, St Andrew's, Scotland sent in a good solution to this problem.
Image
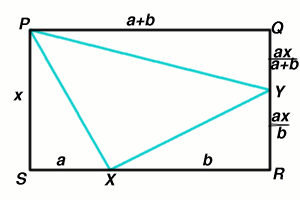
Let $SX = a$ and $XR= b$ then $PQ=a+b$ and, since the areas of the triangles $SPX, XYR$ and $PQY$ are equal, we know that $YR= ax/b$ and $QY = ax/(a+b)$. Because $PS = QR$ we now have $$ \frac{ax}{a+b} + \frac{ax}{b} = x$$ and simplifying this we get $b^2 -ab - a^2 = 0$. So, writing $t$ for $\frac{b}{a}$, we get the quadratic equation $$ t^2 - t - 1 = 0$$ which has roots $$ t = \frac{1 \pm \sqrt 5}{2}$$ but we know that $t$ is positive so $$ t =\frac {1 + \sqrt 5}{2}.$$ Also, writing the ratio $RY/YQ$ in terms of $t$ we get $$ \frac{RY}{YQ} = \frac{a+b}{b} = \frac {1}{t} + 1.$$ We already know that $t=\frac{1}{t} + 1$ because $t^2 = 1 + t$. So $$ \frac{RX}{XS} = \frac {RY}{YQ} = \frac {1 + \sqrt 5}{2}.$$
Teachers' Resources
Why do this problem?
This problem offers opportunities to experience several key problem-solving processes including making a useful transformation into a simpler task and making use of algebra to represent the situation before interpreting results as meaningful solutions within the problem context.Possible approach
Any teaching approach always involves a choice about the level of problem-solving process students are to experience. For example this problem could be used as a guided example of algebraic modelling, but the problem might equally successfully be presented as a simple diagram and students left to make their own progress with the question over time. Both approaches are valid, but the outcomes for the student will be very different with each.Taking a route between those two approaches :
Ask a student to explain what the problem requires, then ask the group for any thoughts about where to start or what might work. Students may choose to work on specified (and simple) rectangle dimensions, hoping to generalise later once they have some results. This is a good and valid strategy.
Before long, try to catch someone questioning whether the rectangle dimensions actually matter. This is a key moment and it is worth stopping the group to allow discussion. We can work with the unit square (which simplifies the task) because areas are only required to match, and any stretch (to create a rectangle) scales all areas by the same factor. This transformation of the problem into a simpler problem is a key mathematical moment. Although students who can see how to proceed without this reduction should be allowed to continue unhindered.
It is possible to use a spreadsheet to explore the change in area distribution.
Through questions and discussion guide students into nominating an independent variable (for example the distance from R to X), and use this to go on to expressing the areas of interest in terms of that variable. If this is pursued algebraically a quadratic equation emerges with two distinct solutions only one of which fits the context being modelled.Key questions :
- What does this problem require ?
- Where might you start - what might work ?
- Would it help to fix on one specific rectangle, or is there another way to start ?
If students have settled on using the Unit Square :
-
Why can this be generalised?
Possible extension :
For more on algebraic modelling try Lap TimesFor more reasoning about triangle areas try Triangle in a Triangle
