Going round in circles
Mathematicians are always looking for efficient methods for solving problems. How efficient can you be?
Problem
Going Round in Circles printable worksheet

Charlie said: "It's Monday today, so it will be Monday again in $7$ days..
and in $770$ days...
and in $140$ days...
and in $35 035$ days...
and in $14 000 000 007$ days!"
Alison said: "and it will be Wednesday in $2$ days...
and in $72$ days...
and in $702$ days...
and in $779$ days...
and in $14 777 002$ days!"
Do you agree with all of Charlie's and Alison's statements?
Charlie and Alison chose numbers that were easy to work with. Can you see why they were chosen?
Can you make up some similar statements of your own?
If today is Monday, what day will it be in $1000$ days' time?
Once you've had a go, have a look at how two students got started on this question:
Ann's Method:
"It will be Monday in $700$ days, $770$ days, $840$ days... "
Can you suggest how Ann might continue?
Luke's Method:
"On my calculator, I can work out that $1000 \div 7 = 142.8571429$.
Then I can work out $142 \times 7$..."
Can you suggest how Luke might continue?
Can you suggest any other methods for solving the problem?
Now try to suggest efficient methods to answer the following questions.
How would you work them out in your head?
What would you do if you had pencil and paper?
How would your method change if you had a calculator?
- If it is autumn now, what season will it be in $100$ seasons?
- If it is November, what month will it be in $1000$ months?
- A railway line has $27$ stations on a circular loop. If I fall asleep and travel through $312$ stations, where will I end up in relation to where I started?
- If it is midday now, will it be light or dark in $539$ hours?
- If a running track is $400$ metres around, where will I be in relation to the start after running 6 miles (approximately $9656$ metres)?
- I was facing North and then spun around through $945 ^\circ$ clockwise. In what direction was I facing at the end?
- If I get on at the bottom of a fairground wheel and the wheel turns through $5000$ degrees, whereabouts on the wheel will I be?
Notes and Background
For more information on calendars and how mathematics can be used to work out quickly days of the week far in the past and future, take a look at the Plus article On What Day Of The Week Were You Born?
Getting Started
You might find it helpful to start by taking a look at the Level 1 and 2 problems in Shifting Times Tables.
Student Solutions
We received lots of great solutions to this question. One student noticed:
If it is Monday today, then in 7 days it will be Monday again, then in 14 days, than 21 and so on. This goes on like the 7 times table: any number divisible by 7 will be a Monday.
If today is Monday, in 29 days what day will it be?
Well, 29/7 = 4 with remainder 1, so in 29 days it will be 1 day after Monday,
i.e. Tuesday. So it matters what the remainder is.
Charlie and Alison's statements were all correct, and we received great explanations of this from Jebin and Matthew from Junior King's School Canterbury, Alastair from St Mary's Primary School in Yorkshire, Cherice from Taipei European School and Sam from Shrewsbury House School. Alastair wrote:
Charlie is right with his numbers because they are all multiples of 7; therefore all will be Mondays. Alison is right because her numbers are all multiples of 7 plus two; therefore all will be Wednesdays.
Lots of students correctly pointed out that, if today is Monday, then in 1000 days it will be Sunday. Anna wrote:
First you must see how many weeks fit into 1000 days, which is 142 weeks and 6 days. Then you must add 142 weeks to Monday, so obviously it will just get you back to Monday. Then, because you still have a remaining 6 days, you must add that to Monday. This will leave you with your answer: Sunday.
Nicholas from Brazil used Ann's method and added on multiples of 7 to get closer to 1000:
It will be Monday in 700 days, 770 days, 840 days, 910 days, 980 days, 987 days and 994 days, and then 6 days later it is Sunday.
Many students also commented on Luke's method. Here is one very clear explanation we received from Yasmine at Garden School, Kuala Lumpur:
First I divided 1000 by 7, which gave 142.8571429. I rounded this down to 142, then multiplied 142 by 7, to give me 994. This means that 994 days is exactly 142 weeks - so in 994 days, it's still Monday. Since we want to know what happens in 1000 days, we just add 6 days to Monday, and find that the answer is Sunday.
George from England pointed out that this is the same as saying that 1000/7 = 142 remainder 6.
We received responses to the later questions from Tom from Monmouth School, Noor-ul-Ain from Westfield Middle School, Sam from Shrewsbury House School, Alastair from St Mary's Primary, and Katherine, Jack, Fred, Megan, Amani, Jasmine, Fiona, Michael, Jet, Markus and Gaeti from Garden School, Kuala Lumpur. Here are some of them:
- If it is autumn now, what season will it be in 100 seasons?
Tom said: there are four seasons, and 4 is a factor of 100, so whatever season it starts off as, it will be the same after 100 seasons. So in 100 seasons it will be autumn again. - If it is November, what month will it be in 1000 months?
Sam answered: on my calculator, 1000/12 = 83.33333333. If I multiply 12 by 83 I get 996. Therefore in 996 months it will be November, so if we add 4 months to that we get March in 1000 months. - A railway line has 27 stations on a circular loop. If I fall asleep and travel through 312 stations, where will I end up in relation to where I started?
Fred and Megan gave this solution:
First you find out how many complete circuits there are in 312 stops: 312/27 = 11.55 loops.
Then you find out how many stops there are in 11 loops: 11×27 = 297 stops.
Next you find out how many further stops they have travelled: 312-297 = 15.
They woke up 15 stations further on than their starting station. - If it is midday now, will it be light or dark in 539 hours?
Sam said: on my calculator 539/24 = 22.4583333. Then 22 × 24 = 528, therefore in 528 hours it will be midday, and 11 hours on from that it will be 539 hours from midday now, so it will be 11 pm. Therefore it will be dark. - If a running track is 400 metres around, where will I be in relation to the start after running 6 miles (approximately 9656 metres)?
Alastair noted: 9656 / 400 = 24.14, and 24 × 400 = 9600, so after 9600 metres I will be back where I started, and after 9656 metres I will be 56 metres around. I was facing North and then spun around through 945$^\circ$ clockwise. In what direction was I facing at the end?
Garden School sent us this helpful explanation and picture:
Image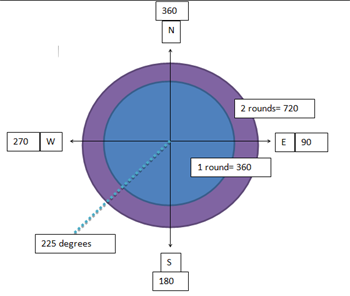
Spinning around twice is the same as spinning through 720$^\circ$, and 945 - 720 = 225, so the required direction is 225 degrees from North, i.e. South-West.- If I get on at the bottom of a fairground wheel and the wheel turns through 5000 degrees, whereabouts on the wheel will I be?
Markus and Gaeti suggested:
First you have to try as get as close to 5000 as you can by multiplying 360 by 13, which is 4680. After 4680$^\circ$ you have come back to where you started. But you still have 320$^\circ$ left to spin through. On a clock face, if the hour hand started off pointing downwards (at 6:00) and spun clockwise through 320$^\circ$ it would be pointing to approximately 4:23.
Teachers' Resources
Why do this problem?
This problem encourages students to consider a range of alternative methods of calculation. There is an opportunity for students to appreciate the importance of the quotient and the remainder when using division to solve a problem. When using calculators, students can explore the relationship between the remainder and the decimal part of the answer.
Possible approach
This printable worksheet may be useful: Going Round in Circles.
Work on this problem complements the ideas introduced in Shifting Times Tables.
Ann's Method:
Can you suggest how Ann might continue?
Luke's Method:
Then I can work out $142 \times 7$..."
Can you suggest how Luke might continue?
Key questions
How can I use what I know (small multiples of 7, 12, 360...) to generate number facts that are not at my fingertips (large multiples of 7, 12, 360...)?
Possible support
Colour Wheels provides a simple context for exploring repeating patterns.
Possible extension
Days and Dates begins in the same way as this problem, but then encourages exploration of the algebra behind modular arithmetic.
