Fractions made faster
Use the fraction wall to compare the size of these fractions -
you'll be amazed how it helps!
Age
7 to 11
Challenge level
Problem
You may like to try our Fractional Wall problem before this one.
Image
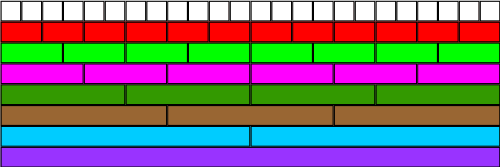
Using the fraction wall above, can you say which is bigger, $\frac{1}{3}$ or $\frac{2}{8}$? By how much?
Which is smaller, $\frac{5}{6}$ or $\frac{3}{4}$? By how much?
What is the difference between $\frac{5}{6}$ and $\frac{1}{3}$?
What is three quarters of $\frac{2}{3}$? Can you explain how you worked this out?
Getting Started
Which rod will you use as the "whole"?
What fraction of this rod are each of the other coloured rods?
What fraction of this rod are each of the other coloured rods?
Student Solutions
Congratulations to Cong, Katie and Charlie
and also Josie, Dominic and George from St Nicolas CE Junior
School, who all sent in correct solutions to this
problem.
George has this to say on finding the larger of two fractions: What you have to do is look at the two fractions and look which is nearest to the right hand side of the wall. Then to find out by how much, you just look at the fraction wall and see which fraction will go in between the two fractions.
Katie's solution can be viewed by clicking here .
George has this to say on finding the larger of two fractions: What you have to do is look at the two fractions and look which is nearest to the right hand side of the wall. Then to find out by how much, you just look at the fraction wall and see which fraction will go in between the two fractions.
Katie's solution can be viewed by clicking here .
Charlie summarises the solution as follows:
$\frac{1}{3}$ is $\frac{2}{24}$ or $\frac{1}{12}$ bigger than
$\frac{2}{8}$
$\frac{3}{4}$ is $\frac{1}{12}$ smaller than $\frac{5}{6}$
$\frac{1}{3}$ is $\frac{3}{6}$ or $\frac{1}{2}$ smaller than
$\frac{5}{6}$
$\frac{3}{4}$ of $\frac{2}{3} = \frac{3}{4}$ of $\frac{8}{12 }=
\frac{6}{12} = \frac{1}{2}$
Teachers' Resources
Fractions Made Faster
You may like to try our Fractional Wall problem before this one.
Image
Using the fraction wall above, can you say which is bigger, $\frac{1}{3}$ or $\frac{2}{8}$? By how much?
Which is smaller, $\frac{5}{6}$ or $\frac{3}{4}$? By how much?
What is the difference between $\frac{5}{6}$ and $\frac{1}{3}$?
What is three quarters of $\frac{2}{3}$? Can you explain how you worked this out?
Having a visual representation of fractions as a wall will aid children's understanding of both equivalent fractions and comparisons of fractions, but perhaps it will also equip them with a method to help them in the future. It is important that pupils have an appreciation of what is being taken as "the whole" and this may need some discussion before the problem as it stands is tackled. Using real Cuisenaire rods to aid manipulation of fractions is invaluable, although the lengths pose some restrictions. However, OHT rods could be used as a way into the problem by concentrating on just a few different lengths to start with.
This could be used to help older children to understand the concepts necessary for manipulating fractions to add and subtract them. It is amazing how much easier the visualisation makes the arithmetic process. Just try it yourself and see.