Dodecagon angles
Weekly Problem 50 - 2012
The diagram shows a regular dodecagon. What is the size of the marked angle?
The diagram shows a regular dodecagon. What is the size of the marked angle?
Problem
The diagram shows a regular dodecagon (a polygon with twelve equal sides and equal angles).
Image
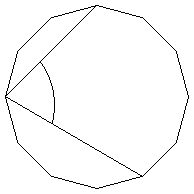
What is the size of the marked angle?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Each side of the dodecagon subtends an angle of $30^{\circ}$ at the centre of the circumcircle of the figure (the circle which passes through all $12$ of its vertices).
Image
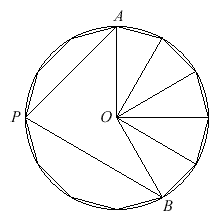
$$\angle AOP = 90^{\circ}$$ so $$\angle OPA = 45^{\circ}$$
$$\angle BOP = 120^{\circ}$$ so $$\angle OPB = 30^{\circ}$$ Therefore $$\angle APB = 45^{\circ} + 30^{\circ} = 75^{\circ}$$ Alternatively, $$\angle AOB = 150^{\circ}$$ and, as the angle subtended by an arc at the centre of a circle is twice the angle subtended by that arc at a point on the circumference, $$\angle APB = 75^{\circ}$$
