Consecutive negative numbers
Problem
Consecutive Negative Numbers printable worksheet
Do you notice anything about the solutions when you add and/or subtract consecutive negative numbers?
Take, for example, four consecutive negative numbers, say $$-7, -6, -5, -4$$ Now place $+$ and/or $-$ signs between them.
e.g.
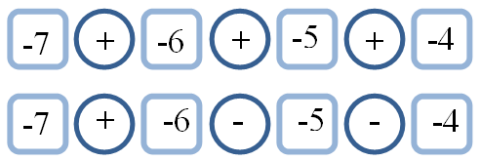
There are many more possibilities. Try to list all of them.
Now work out the solutions to the various calculations.
e.g.
Choose a different set of four consecutive negative numbers and repeat the process.
Take a look at both sets of solutions. Notice anything?
Can you explain any similarities?
Can you predict some of the solutions you will get when you start with a different set of four consecutive negative numbers?
Test out any conjectures you may have.
Can you explain and justify your findings?
Getting Started
Do you notice anything about the solutions when you add and/or subtract consecutive positive numbers?
You could start by considering four consecutive positive numbers before moving on to consider four consecutive negative numbers.
If you have looked at several sets of consecutive numbers and noticed some similarities in the solutions, you may be wanting to explain why they occur. An algebraic representation of the situation might help you with this:
if $a$ is your smallest number, the four consecutive numbers are $a$, $a+1$, $a+2$, $a+3$
Student Solutions
Well done to Edison, from STC School in Hong Kong, and to Esther, who both sent us correct solutions. Here is Esther's solution:
| Operations | -8, -7, -6, -5 | -10, -9, -8, -7 | Formula |
| + + + | -26 | -34 | 4n + 6 |
| + + - | -16 | -20 | 2n |
| + - + | -14 | -18 | 2n + 2 |
| + - - | -4 | -4 | -4 |
| - + + | -12 | -16 | 2n + 4 |
| - + - | -2 | -2 | -2 |
| - - + | 0 | 0 | 0 |
| - - - | 10 | 14 | -2n - 6 |
Teachers' Resources
This is a variation on the problem Consecutive Numbers . Teachers may need to choose between the two problems - doing both may involve too much overlap.
Why do this problem?
This problem could replace a "standard practice exercise" for adding and subtracting negative numbers. It provides opportunities for a lot of calculation, in a context of experimenting, conjecturing, testing conjectures, etc.
Possible approach
This printable worksheet may be useful: Consecutive Negative Numbers.
Ask for four consecutive negative numbers, write them on the board, then place $+$ and/or $-$ signs in the three gaps between them. "Assuming we are only allowed to add and subtract, how else could the gaps be filled?" Make a note of the suggestions until students are confident that all possibilities have been listed. "How do we know we have listed them all?"
To direct attention to more than just routine calculation, collate sets of some students' results on the board, and ask the group for general descriptive comments - encouraging conjectures and explanations. Students can then go back to working in pairs to test the validity of what they have heard suggested.
Encourage students to move from "there's always a zero" to the reason why this is true - isolate and examine the cases where it is zero.
At the end of the lesson a plenary discussion can offer students a chance to present their findings, explanations and proofs.
Key questions
How do you know you have considered all the possible calculations?
Do the answers seem random, or can any/all be predicted?
How do you KNOW that what you say will ALWAYS work?
Possible support
Students could use Consecutive Numbers for a similar problem which offers opportunities to experiment/conjecture/justify but doesn't require negative numbers.
Students could start by considering the solutions when they add and/or subtract three consecutive negative numbers.
Teachers may like to take a look at the article Adding and Subtracting Negative Numbers
Possible extension
What happens if we allow a $+$ or a $-$ sign before the first number?
What happens if it doesn't have to be FOUR consecutive negatives?