Changing areas, changing perimeters
Changing Areas, Changing Perimeters printable sheets: Instructions, Shapes, Dimensions
Here are nine shapes. You can download a set of these shapes to print off here.
|
Image
|
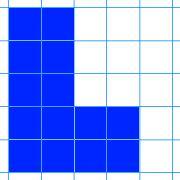
Image
|
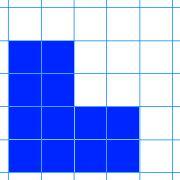
Image
|
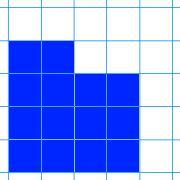
| Image
|
Image
|
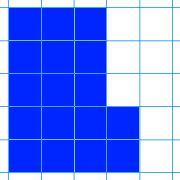
Image
|
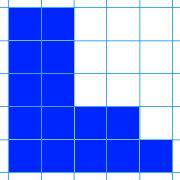
| Image
|
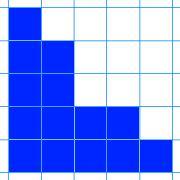
Image
|
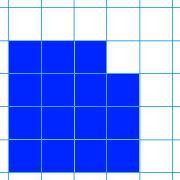
Image
|
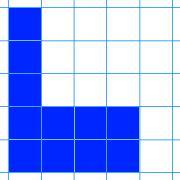
The challenge is to arrange the shapes in a 3 by 3 grid like the one below:
As you go from left to right, the area of the shapes must increase.
As you go from top to bottom, the perimeter of the shapes must increase.
All the shapes in the middle column must have the same area.
All the shapes on the middle row must have the same perimeter.
What reasoning can you use to help you to decide where each card must go?
Here are the dimensions of nine rectangles (printable version here).
|
$2$ by $8$
rectangle
|
$4$ by $4$
square
|
$1$ by $15$
rectangle
|
|
$5$ by $5$
square
|
$3$ by $8$
rectangle
|
$2$ by $7$
rectangle
|
|
$1$ by $16$
rectangle
|
$3$ by $6$
rectangle
|
$1$ by $9$
rectangle
|
Can you arrange them in the grid in the same way?
Once you've placed the nine cards, take a look at the extended grid below:
The ticks represent the nine cards you've already placed.
Can you create cards with dimensions for rectangles that could go in the four blank spaces that satisfy the same criteria?
Not all the spaces are possible to fill. Can you explain why?
Can you produce a set of cards that could be arranged in the same way, if the card in the centre is a 1 by 5 rectangle?
Working on Area and Perimeter might give you some useful insights to help you to solve this problem.
If you are having trouble making sense of the grid, have a look at this image. The robots have been arranged according to their width and height, in the same way that the cards need to be arranged according to their area and perimeter:
As you go from left to right, the width of the robots increases.
As you go from top to bottom, the height of the robots increases.
All the robots in the middle column have the same width.
All the robots on the middle row have the same height.
Isabelle from South Wilts and Natalie from St.Andrews International School in Thailand both answered the first challenge correctly.
Here is Natalie's arrangement of the shapes:
Here is how Isabelle described her strategy:
a) Write down the areas and perimeters of each shape.
b) The only three shapes that share an area are G, A & C therefore they must occupy the middle column.
c) B, D & I have areas less than 14 so must occupy the left column and E, F & H have areas greater than 14 so must occupy the right column.
d) The shapes with perimeter 20 (B, C & H) must go in the bottom row, those with perimeter 18 must go in the middle row and those with perimeter 16 must go in the top row.
There is only one way this can be achieved so by a process of elimination the solution is as above.
Isabelle also answered the second challenge correctly:
| AREA | ||||
|---|---|---|---|---|
| - | = | + | ||
| - | 2 by 7 | 4 by 4 | 3 by 6 | |
| PERIMETER | = | 1 by 9 | 2 by 8 | 5 by 5 |
| + | 1 by 15 | 1 by 16 |
3 by 8
|
It's possible to fill in the box on the left too. I wonder if you can think of a way, and convince yourself that it's impossible to fill in the top and right boxes.
Why do this problem?
Working on this problem will give students a deeper understanding of area and perimeter, and how they change as a shape is altered. The problem will address some students' misconception that as area increases, perimeter must necessarily increase too.
Possible approach
Display a simple shape made out of squares on a small square grid:
As each pair finishes, they can be given the second set of cards to work on in the same way. For those who finish quickly, ask them the question from the problem about extending the grid like this:
Towards the end of the lesson, bring the class together to share any efficient ways they found to compare areas and perimeters without having to work them all out.
In sharing feedback on the first activity, ask students what they notice about the shapes on the top row of the grid.
To explain why all shapes drawn by cutting corners out of a 4 by 4 square have a perimeter of 16, these images might be useful:
"How much perimeter has been lost by cutting out the pink rectangle? How much has been gained?"
Shapes on the second and third row can be compared in the same way.
For the second activity, we want students to recognise:
"Rectangles that are closer to squares have smaller perimeters than long thin rectangles with the same area"
One prompt that could draw out this thinking might be:
"If two rectangles have the same area but different perimeters, how can I decide which has the greater perimeter?"
Finally, discuss the possible content of the four extra spaces in the extended grid, focussing in particular on why some of the spaces are impossible to fill in.
Possible support
Area and Perimeter provides a good starting point for the thinking expected of students in this problem.
Possible extension
Finally, students could be challenged to create their own set of cards with a $1$ by $5$ rectangle as the central card. This forces them to consider rectangles whose side lengths are not whole numbers.