Bisector intersection
Weekly Problem 14 - 2007
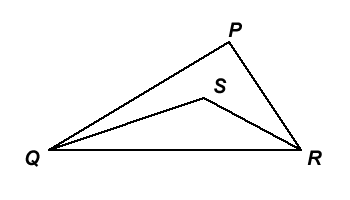
In the triangle PQR, the angle QPR=40degrees and the internal bisectors of the angles at Q and R meet at S, as shown. What is the size of angle QSR?
In the triangle PQR, the angle QPR=40degrees and the internal bisectors of the angles at Q and R meet at S, as shown. What is the size of angle QSR?
Age
11 to 16
Challenge level
Problem
Image
(Diagram not to scale.)
In the triangle $PQR$, the angle $QPR=40^{\circ}$ and the internal bisectors of the angles at $Q$ and $R$ meet at $S$, as shown. What is the size of angle $QSR$?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
$110^{\circ}$
As $\angle QPR=40^{\circ}$, $\angle PQR+\angle PRQ=180^{\circ}-40^{\circ} =140^{\circ}$.
So $\angle SQR+\angle SRQ=140^{\circ}/2=70^{\circ}$. Therefore $\angle QSR =180^{\circ}-70^{\circ}=110^{\circ}$.