Successful mathematicians understand curriculum concepts, are fluent in mathematical procedures, can solve problems, explain and justify their thinking, and have a positive attitude towards learning mathematics.
The rope model* below offers an image of how we can characterise good mathematicians. Each strand complements the others and contributes to the strength of the rope in equal measure. If our students are to think and work as mathematicians, we need to offer them opportunities to develop all three strands.
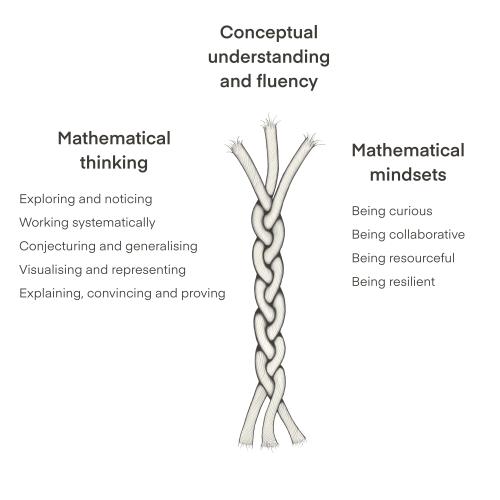
Challenging students with rich tasks strengthens students' conceptual understanding and procedural fluency. Our Primary and Secondary mapping documents link our rich tasks to the different curriculum areas.
If students are going to be good mathematicians, they also need opportunities to develop desirable mathematical mindsets. Our rich tasks encourage students to be curious, collaborative, resourceful and resilient, so that in turn, they can feel positive about their ability to make progress.
The final strand of our rope model recognises the importance of mathematical thinking. Rich tasks offer students opportunities to explore, question, work systematically, conjecture, visualise, communicate, generalise, create convincing arguments...
NRICH tasks recognise the importance of all three strands and aim to strengthen students in all three areas, by challenging them to think and work as mathematicians.
Our Primary teachers landing page is structured to reflect the three strands of the rope model:
Problems arranged by curriculum topics
Problems arranged by mathematical thinking skills
Problems arranged by mathematical mindsets
Our Secondary teachers landing page is structured to reflect the three strands of the rope model:
Problems arranged by curriculum topics
Problems arranged by mathematical thinking skills
Problems arranged by mathematical mindsets
Guidance is available for teachers wanting to develop their students' mathematical thinking skills, and nurture their mathematical mindsets.
Alan Wigley's Challenging Model for Teaching Mathematics describes how these problems could be used in the classroom.
* The rope model developed by Kilpatrick et al has informed our thinking and influenced how we have chosen to structure the NRICH website. You can read more about Kilpatrick et al's model in chapter 4 of their book, Adding it Up - Helping Children Learn Mathematics (2001)